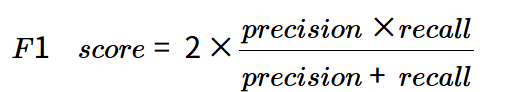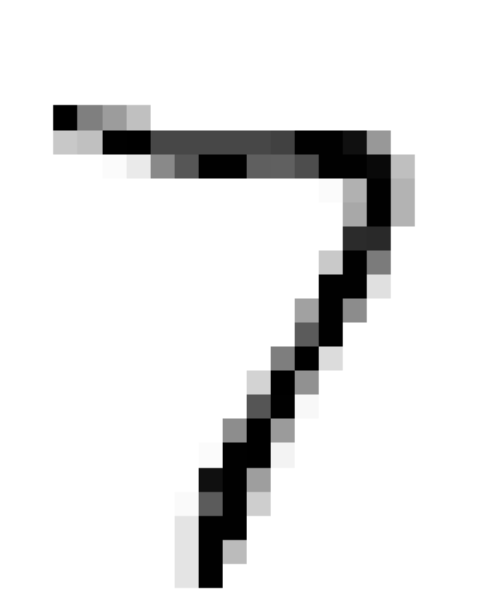3장. 분류
3.1 MNIST
⭐기본적으로 사이킷런은 내려받은 데이터셋을 사용자 홈 디렉터리 안의 scikit_learn_data 디렉터리에 캐싱한다.
🔖data 다운로드
1
2
3
4
5
6
7
8
9
from sklearn.datasets import fetch_openml
# 사이킷런 1.2에서 추가된 parser 매개변수 기본값이 1.4 버전에서 'liac-arff'에서 'auto'로 바뀝니다.
# 'auto'일 경우 희소한 ARFF 포맷일 때는 'liac-arff', 그렇지 않을 때는 'pandas'가 됩니다.
# 이에 대한 경고를 피하려면 parser='auto'로 지정하세요.
mnist = fetch_openml('mnist_784', as_frame=False)
mnist.keys() # Sklearn.utils.Bunch 객체일때 뭐 있나 확인 가능.
X, y = mnist.data, mnist.target
💡Sklearn.datasets 패키지에 있는 함수
o fetch_* 함수: 실전 데이터셋을 다운로드 (ex. fetch_openml())
o load_* 함수: 사이킷런에 번들로 포함된 소규모 데이터셋을 로드하기 위한 함수
o make_* 함수: 테스트에 유용한 가짜 데이터셋을 생성하기 위한 함수
=> 생성된 데이터셋은 일반적으로 넘파이 배열, 입력과 타깃 데이터를 담은 (X, y) 튜플로 반환.
=> sklearn.utils.Bunch 객체로 반환될 수도!
💡Sklearn.utils.Bunch 객체
이 객체는 속성으로 다음과 같은 항목을 참조할 수 있는 딕셔너리
o DESCR: 데이터셋 설명
o data: 입력 데이터, 일반적으로 2D 넘파이 배열
o target: 레이블, 일반적으로 1D 넘파이 배열
💡fetch_openml()
o 기본적으로 입력을 판다스 데이터프레임, 레이블을 시리즈로 반환.
BUT! MNIST 데이터셋은 이미지임로 df이 잘 맞지 않다. 따라서 as_frame=False로 지정하여 넘파이 배열로 데이터를 받음.
🔖이미지 보기
1
2
3
4
5
6
7
8
9
10
11
import matplotlib.pyplot as plt
def plot_digit(image_data):
image = image_data.reshape(28, 28) # 2차원으로 바꾸고
plt.imshow(image, cmap="binary") # 흑백으로 출력력
plt.axis("off") # 축 안보여주기!
some_digit = X[0]
plot_digit(some_digit)
save_fig("some_digit_plot") # 추가 코드
plt.show()
🔖자세히 보기 전!!!! 테스트 세트 떼어놓기!!!!
1
2
3
# MNIST는 사실 미리 나누어져 있음ㅎ
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
3.2 이진 분류기 훈련
❗’5-감지기’는 ‘5’와 ‘5 아님’ 두 개의 클래스를 구분할 수 있는 이진 분류기 이다.
🔖타깃 벡터 만들기!
1
2
y_train_5 = (y_train == '5') # 5는 True고, 다른 숫자는 모두 False
y_test_5 = (y_test == '5')
🔖SGD(확률적 경사 하강법) 훈련 시키기
💡SGD 분류기?
o 한 번에 하나씩 훈련 샘플을 독립적으로 처리할 수 있음.(온라인 학습에 잘 들어맞음)
o 매우 큰 데이터셋을 효율적으로 처리할 수 있음.
1
2
3
4
from sklearn.linear_model import SGDClassifier
sgd_clf = SGDClassifier(random_state=42)
sgd_clf.fit(X_train, y_train_5)
3.3 성능 측정
❗ 분류기 평가는 회귀 모델보다 훨씬 어려움!
3.3.1 교차 검증을 사용한 정확도 측정
🔖교차 검증 구현
- 사이킷런이 제공하는 기능보다 교차 검증 과정을 더 많이 제어해야 하면, 직접 구현해봐야함!!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from sklearn.model_selection import StratifiedKFold
from sklearn.base import clone
skfolds = StratifiedKFold(n_splits=3)
# 데이터가 미리 섞여있지 않다면, shuffle=True 추가
# StratifiedKFold는 클래스별 비율이 유지되도록 폴드를 만듦.
for train_index, test_index in skfolds.split(X_train, y_train_5):
clone_clf = clone(sgd_clf) # 모델 복사
X_train_folds = X_train[train_index]
y_train_folds = y_train_5[train_index]
X_test_fold = X_train[test_index]
y_test_fold = y_train_5[test_index]
clone_clf.fit(X_train_folds, y_train_folds)
y_pred = clone_clf.predict(X_test_fold)
n_correct = sum(y_pred==y_test_fold)
print(n_correct / len(y_pred))
🔖교차 검증 수행
1
2
3
4
from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")
# array([0.95035, 0.96035, 0.9604 ])
모든 이미지를 가장 많이 등장하는 클래스(여기서는 음성 클래스, 즉 ‘5 아님’)로 분류하는 더미 분류기를 만들어 비교!!
1
2
3
4
5
6
7
8
from sklearn.dummy import DummyClassifier
dummy_clf = DummyClassifier()
dummy_clf.fit(X_train, y_train_5)
print(any(dummy_clf.predict(X_train)))
cross_val_score(dummy_clf, X_train, y_train_5, cv=3, scoring="accuracy")
# array([0.90965, 0.90965, 0.90965])
💡더미 분류기란??
o “실제 머신러닝 모델이 아니라, 단순한 기준(rule)으로 분류하는 매우 단순한 모델!” “실제 모델과 비교하기 위해 사용됨!”
💬 특히, 불균형한 데이터셋을 다룰 때, 정확도를 분류기의 성능 측정 지표로 선호하지 않음.
💬 분류기의 성능을 평가할땐 오차 행렬이 더 좋음!!
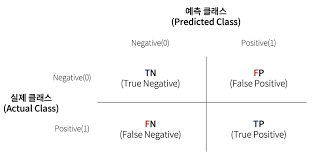
3.2.2 오차 행렬
❗ 테스트 세트로 예측을 만들 수 있지만, 여기서 이용하면 안됨!!!(테스트 세트는 프로젝트의 맨 마지막에 분류기가 출시 준비 마치고 이용!!)
1
2
3
4
5
6
7
8
9
10
11
from sklearn.model_selection import cross_val_predict
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
# 훈련 세트의 모든 샘플에 대해 깨끗한 예측을 얻게 됨.
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_train_5, y_train_pred)
cm
# array([[53892, 687],
# [ 1891, 3530]])
- 행: 실제 클래스 / 열: 예측한 클래스
- 첫 번째 행: 음성 클래스
- 진짜 음성(첫 번째 행의 첫 번째 열)
- 거짓 양성 or 1종 오류(첫 번째 행의 두 번째 열)
- 두 번째 행: 양성 클래스
- 거짓 음성 or 2종 오류(두 번째 행의 첫 번째 열)
- 진짜 양성(두 번째 행의 두 번째 열)
- 첫 번째 행: 음성 클래스
1
2
3
4
5
y_train_perfect_predictions = y_train_5 # 완벽한 분류기일 경우
confusion_matrix(y_train_5, y_train_perfect_predictions)
#array([[54579, 0],
# [ 0, 5421]], dtype=int64)
# 완벽하면 주대각선만 0이 아닌 값이 된다.
🔖오차 행렬의 지표
- 정밀도(양성 예측의 정확도)
- TP / (FP + TP)
- 올리는 가장 쉬운 방법: 제일 확신이 높은 샘플에 대해 양성 예측을 하고 나머지는 모두 음성 예측을 하는 분류기
- 재현율(민감도 or 진짜 양성 비율)
- TP / (TP + FN)
3.3.3 정밀도와 재현율
🔖F1 점수
- 정밀도와 재현율의 조화 평균(보통의 평균은 모든 값을 동일하게 취급하지만, 조화 평균은 낮은 값에 훨씬 높은 비중을 둠).
1
2
3
from sklearn.metrics import f1_score
f1_score(y_train_5, y_train_pred)
❗정밀도와 재현율이 비슷한 분류기(F1 점수 높음)가 항상 바람직한 것은 아니다. 상황에 따라 정밀도가 중요할 수도 있고, 재현율이 중요할 수도 있다.
❗ 정밀도/재현율 트레이드오프
3.3.4 정밀도/재현율 트레이드 오프
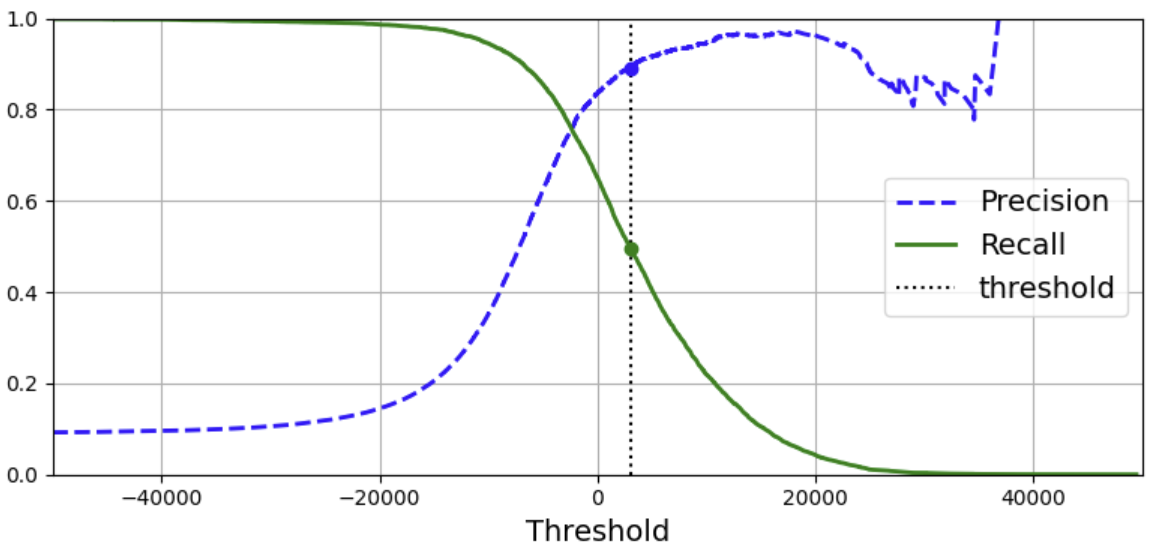
❗임계값이 높을 수록, 재현율은 낮아지고 반대로 정밀도는 높아진다.
- decision_function() 메서드: 각 샘플의 점수를 얻을 수 있음.
1
2
3
4
5
6
7
8
9
10
11
y_scores = sgd_clf.decision_function([some_digit])
y_scores
threshold = 0
y_some_digit_pred = (y_scores > threshold)
y_some_digit_pred
# True
threshold = 3000
y_some_digit_pred = (y_scores > threshold)
y_some_digit_pred
# False
🔖 적절한 임계값 구하기!
cross_val_predict(): 훈련 세트에 있는 모든 샘플의 점수 구하기.
precision_recall_curve(): 가능한 모든 임곗값에 대해 정밀도와 재현율 구함(이 함수는 무한한 임곗값에 해당하는 값으로 마지막 정밀도에 1을, 마지막 재현율에 0을 추가한다.)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function")
# 이번엔 예측이 아닌 결정 점수 반환
from sklearn.metrics import precision_recall_curve
precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)
plt.figure(figsize=(8, 4)) # 추가 코드
plt.plot(thresholds, precisions[:-1], "b--", label="Precision", linewidth=2)
plt.plot(thresholds, recalls[:-1], "g-", label="Recall", linewidth=2)
plt.vlines(threshold, 0, 1.0, "k", "dotted", label="threshold")
# 추가 코드 – 그림 3–5를 그리고 저장합니다
idx = (thresholds >= threshold).argmax() # 첫 번째 index ≥ threshold
plt.plot(thresholds[idx], precisions[idx], "bo")
plt.plot(thresholds[idx], recalls[idx], "go")
plt.axis([-50000, 50000, 0, 1])
plt.grid()
plt.xlabel("Threshold")
plt.legend(loc="center right")
save_fig("precision_recall_vs_threshold_plot")
plt.show()
⭐임계값이 올라가면, 재현율은 낮아질 수밖에 없고 정밀도는 올라갈 수도? 내려갈 수도 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import matplotlib.patches as patches # 추가 코드 – 구부러진 화살표를 그리기 위해서
plt.figure(figsize=(6, 5)) # 추가 코드
plt.plot(recalls, precisions, linewidth=2, label="Precision/Recall curve")
# extra code – just beautifies and saves Figure 3–6
plt.plot([recalls[idx], recalls[idx]], [0., precisions[idx]], "k:")
plt.plot([0.0, recalls[idx]], [precisions[idx], precisions[idx]], "k:")
plt.plot([recalls[idx]], [precisions[idx]], "ko",
label="Point at threshold 3,000")
plt.gca().add_patch(patches.FancyArrowPatch(
(0.79, 0.60), (0.61, 0.78),
connectionstyle="arc3,rad=.2",
arrowstyle="Simple, tail_width=1.5, head_width=8, head_length=10",
color="#444444"))
plt.text(0.56, 0.62, "Higher\nthreshold", color="#333333")
plt.xlabel("Recall")
plt.ylabel("Precision")
plt.axis([0, 1, 0, 1])
plt.grid()
plt.legend(loc="lower left")
save_fig("precision_vs_recall_plot")
plt.show()
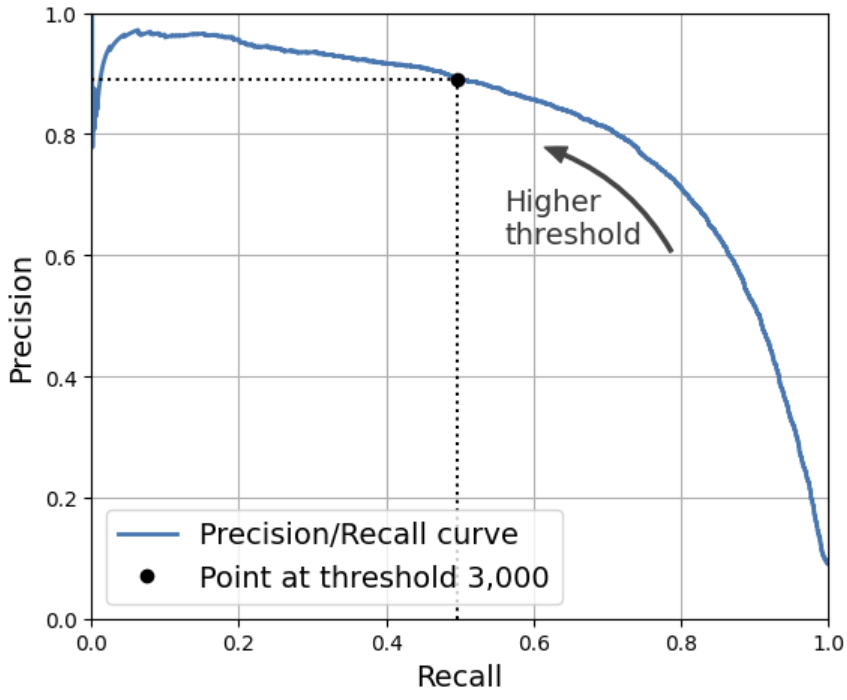
⭐정밀도의 급 하강점 직전을 정밀도/재현율 트레이드오프로 선택하는 것이 좋음.
1
2
3
4
idx_for_90_precision = (precisions >= 0.90).argmax()
threshold_for_90_precision = thresholds[idx_for_90_precision]
threshold_for_90_precision
# 3370.0194991439557
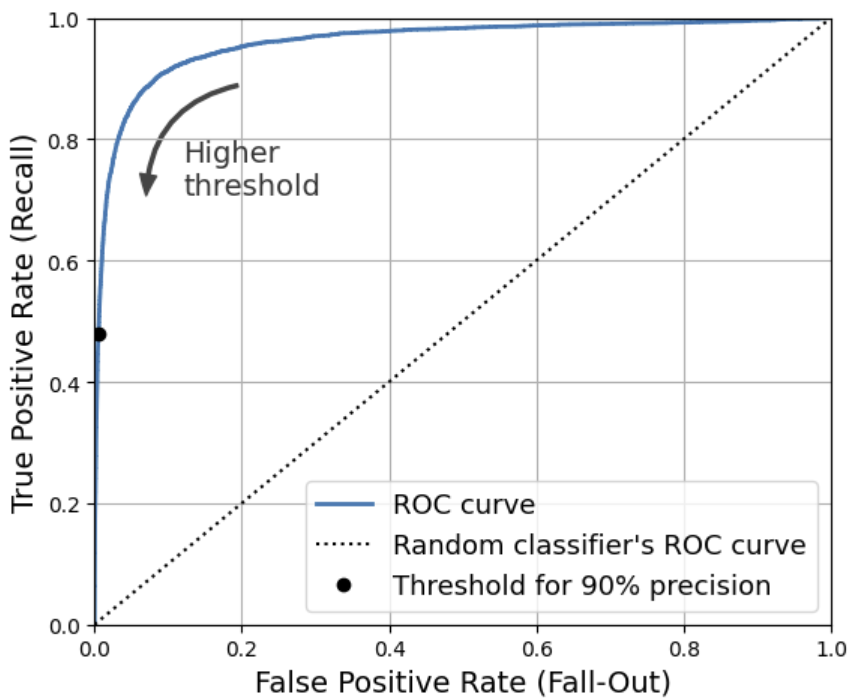
3.3.5 ROC 곡선
🔖ROC 곡선이란?
- 거짓 양성 비율(FPR)에 대한 진짜 양성 비율(TPR - 재현율)
- 재현율(민감도)에 대한 1-특이도(특이도 - TNR) 그래프
🔖ROC 곡선 그리기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)
idx_for_threshold_at_90 = (thresholds <= threshold_for_90_precision).argmax()
# 임계값이 내림으로 되어있기에...
tpr_90, fpr_90 = tpr[idx_for_threshold_at_90], fpr[idx_for_threshold_at_90]
plt.figure(figsize=(6, 5)) # 추가 코드
plt.plot(fpr, tpr, linewidth=2, label="ROC curve")
plt.plot([0, 1], [0, 1], 'k:', label="Random classifier's ROC curve")
plt.plot([fpr_90], [tpr_90], "ko", label="Threshold for 90% precision")
# 추가 코드 – 그림 3–7을 그리고 저장합니다
plt.gca().add_patch(patches.FancyArrowPatch(
(0.20, 0.89), (0.07, 0.70),
connectionstyle="arc3,rad=.4",
arrowstyle="Simple, tail_width=1.5, head_width=8, head_length=10",
color="#444444"))
plt.text(0.12, 0.71, "Higher\nthreshold", color="#333333")
plt.xlabel('False Positive Rate (Fall-Out)')
plt.ylabel('True Positive Rate (Recall)')
plt.grid()
plt.axis([0, 1, 0, 1])
plt.legend(loc="lower right", fontsize=13)
save_fig("roc_curve_plot")
plt.show()
🔖 AUC
- AUC(곡선 아래의 면적)
- 완벽한 분류기는 ROC의 AUC가 1이고, 완전한 랜덤 분류기는 0.5 입니다.
1
2
3
4
from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5, y_scores)
# 0.96
💡ROC? 정밀도/재현율 곡선?
o 양성 클래스가 드물거나 거짓 음성보다 거짓 양성이 더 중요할 때 PR(정밀도/재현율 곡선) <-> 그렇지 않으면 ROC!
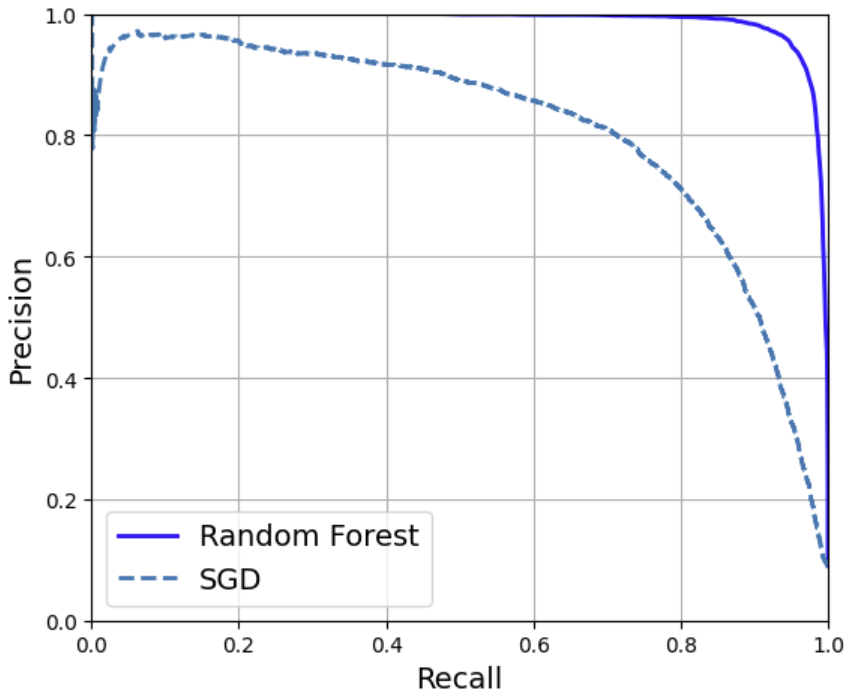
🔖RandomForestClassifier와 SGDClassifier의 PR곡선과 F1 비교
1
2
3
from sklearn.ensemble import RandomForestClassifier
forest_clf = RandomForestClassifier(random_state=42)
- predict_proba(): 각 샘플에 대한 클래스 확률(작동 방식 때문에 decision_function() 제공 X)
- 양성 클래스에 대한 점수 이용
1
y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3,method="predict_proba")
💡추정확률
o 이는 실제 확률X 추정 확률!
o sklearn.calibration 패키지에는 추정 확률을 보정하여 실제 확률에 훨씬 가깝게 만드는 도구 있음.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
y_scores_forest = y_probas_forest[:, 1]
precisions_forest, recalls_forest, thresholds_forest = precision_recall_curve(
y_train_5, y_scores_forest)
plt.figure(figsize=(6, 5)) # 추가 코드
plt.plot(recalls_forest, precisions_forest, "b-", linewidth=2,
label="Random Forest")
plt.plot(recalls, precisions, "--", linewidth=2, label="SGD")
# 추가 코드 – 그림 3–8을 그리고 저장합니다
plt.xlabel("Recall")
plt.ylabel("Precision")
plt.axis([0, 1, 0, 1])
plt.grid()
plt.legend(loc="lower left")
save_fig("pr_curve_comparison_plot")
plt.show()
3.4 다중 분류
- 다중 분류기(다항 분류기): 둘 이상의 클래스를 비교할 수 있음.
- LogisticRegression, RandomForestClassifier, GaussianNB 등은 가능!
- SGDClassifier와 SVC와 같은 다른 알고리즘은 이진 분류만 가능.
- BUT!! 이진 분류기를 여러 개 사용해 다중 클래스를 분류하는 기법도 많다.
- OvR or Ova: 각 클래스마다 이진 분류를 훈련시킨뒤, 이미지를 분류할 때 각 분류기의 결정 점수 중에서 가장 높은 것을 클래스로!
- OvO: 0과 1 구별, 0과 2 구별 등과 같이 각 숫자의 조합마다 이진 분류기를 훈련시키는 것! 클래스가 N개라면 분류기는 N x (N-1) / 2개가 필요!
- BUT!! 이진 분류기를 여러 개 사용해 다중 클래스를 분류하는 기법도 많다.
🔖서포트 벡터 머신 분류기
1
2
3
4
from sklearn.svm import SVC
svm_clf = SVC(random_state=42)
svm_clf.fit(X_train[:2000], y_train[:2000]) # y_train_5가 아니고 y_train을 사용합니다.
이때, 사이킷런은 OvO 전략을 이용해 45개의 이진 분류기를 훈련!
1
svm_clf.predict([some_digit])
1
2
3
some_digit_scores = svm_clf.decision_function([some_digit])
some_digit_scores.round(2)
# array([[ 3.79, 0.73, 6.06, 8.3 , -0.29, 9.3 , 1.75, 2.77, 7.21, 4.82]])
이때, 각 클래스는 동률 문제를 해결 하기 위해 분류기 점수를 기반으로 각 쌍에서 이긴 횟수에 약간의 조정 값(최대 +-0.33)을 더하거나 뺀 점수를 얻는다.
1
2
3
4
5
6
7
8
9
10
11
12
class_id = some_digit_scores.argmax()
class_id
svm_clf.classes_
# array(['0', '1', '2', '3', '4', '5', '6', '7', '8', '9'], dtype=object)
svm_clf.classes_[class_id]
# 추가 코드 – 45개 OvO 점수를 얻는 방법
svm_clf.decision_function_shape = "ovo"
some_digit_scores_ovo = svm_clf.decision_function([some_digit])
some_digit_scores_ovo.round(2)
❗ 근데 이렇게 인덱스 값과 값이 같은 경우는 드물다!
🔖OneVsOneClassifier나 OneVsRestClassifier
- 이진 분류기 인스턴스를 만들어 객체를 생성할 때 전달하면 됩니다(이진 분류기일 필요X)
1
2
3
4
5
6
7
8
9
10
11
from sklearn.multiclass import OneVsRestClassifier
ovr_clf = OneVsRestClassifier(SVC(random_state=42))
ovr_clf.fit(X_train[:2000], y_train[:2000])
ovr_clf.predict([some_digit])
# 5
len(ovr_clf.estimators_)
# 10
# 추정기 갯수
🔖다중 분류 dataset에 SGDClassifier 훈련하기
1
2
3
4
5
6
7
sgd_clf = SGDClassifier(random_state=42)
sgd_clf.fit(X_train, y_train)
sgd_clf.predict([some_digit])
# 3
sgd_clf.decision_function([some_digit]).round()
# array([[-31893., -34420., -9531., 1824., -22320., -1386., -26189., -16148., -4604., -12051.]])
1
2
3
# 평가하기
cross_val_score(sgd_clf, X_train, y_train, cv=3, scoring="accuracy")
#array([0.87365, 0.85835, 0.8689 ])
나쁘진 않지만! 입력 스케일을 조정해보자!
1
2
3
4
5
6
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train.astype("float64"))
cross_val_score(sgd_clf, X_train_scaled, y_train, cv=3, scoring="accuracy")
# array([0.8983, 0.891 , 0.9018])
3.5 오류 분석
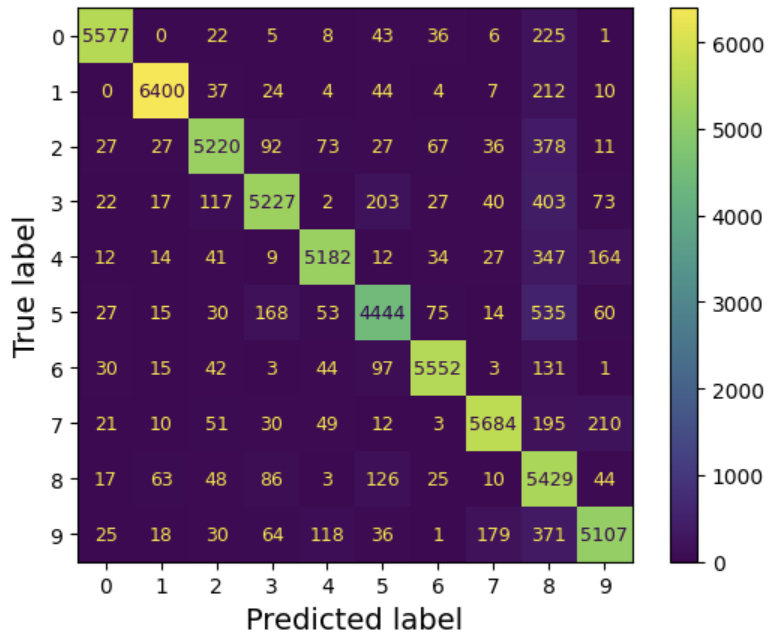
🔖오차 행렬 살펴보기
1
2
3
4
5
6
from sklearn.metrics import ConfusionMatrixDisplay
y_train_pred = cross_val_predict(sgd_clf, X_train_scaled, y_train, cv=3)
plt.rc('font', size=9) # 추가 코드 - 폰트 크기를 줄입니다
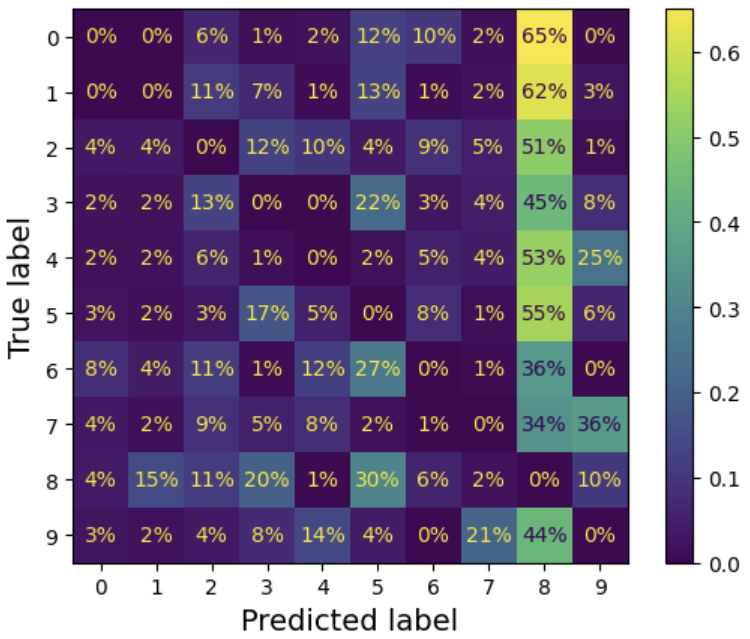
ConfusionMatrixDisplay.from_predictions(y_train, y_train_pred)
plt.show()
여기서 5번 행과 5번 열의 대각선에 있는 셀은 다른 숫자보다 약간 더 어둡게 보임. 이는 모델이 5에서 더 많은 오류를 범했거나 다른 숫자보다 5가 적기 때문이다.
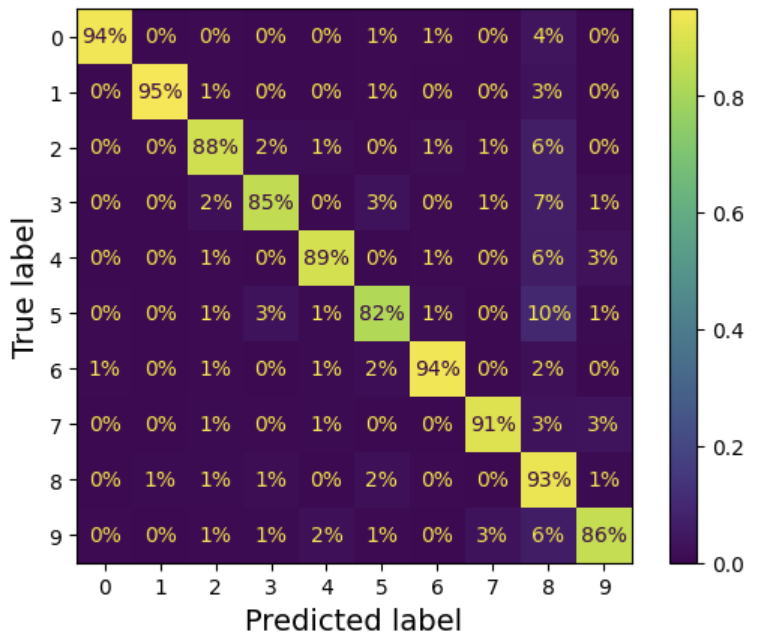
=> 각 값을 해당 클래스(True 레이블)의 총 이미지 수로 나누어 정규화!!
1
2
3
4
plt.rc('font', size=10) # 추가 코드
ConfusionMatrixDisplay.from_predictions(y_train, y_train_pred,
normalize="true", values_format=".0%")
plt.show()
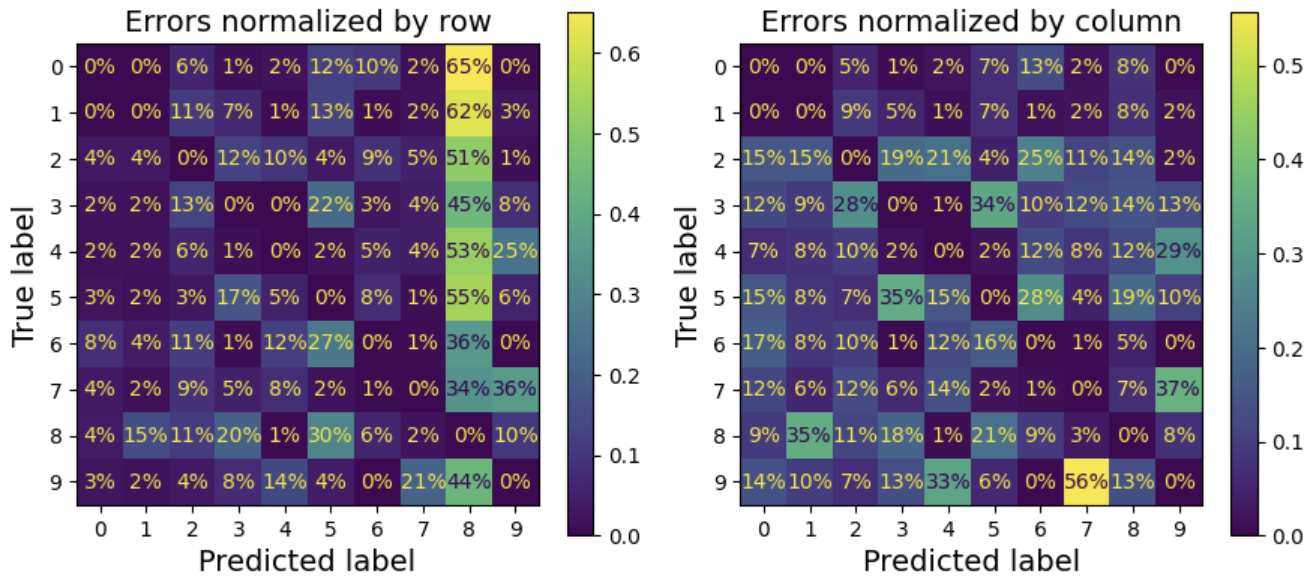
오류를 더 눈에 띄게 만들고 싶다면 올바른 예측에 대한 가중치를 0으로 설정!
1
2
3
4
5
6
sample_weight = (y_train_pred != y_train)
plt.rc('font', size=10) # 추가 코드
ConfusionMatrixDisplay.from_predictions(y_train, y_train_pred,
sample_weight=sample_weight,
normalize="true", values_format=".0%")
plt.show()
행 단위가 아닌 열 단위로 정규화 해보자!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 추가 코드 – 그림 3–10을 생성하고 저장합니다
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(9, 4))
plt.rc('font', size=10)
ConfusionMatrixDisplay.from_predictions(y_train, y_train_pred, ax=axs[0],sample_weight=sample_weight
normalize="true", values_format=".0%")
axs[0].set_title("Errors normalized by row")
ConfusionMatrixDisplay.from_predictions(y_train, y_train_pred, ax=axs[1],sample_weight=sample_weight,
normalize="pred", values_format=".0%")
axs[1].set_title("Errors normalized by column")
save_fig("confusion_matrix_plot_2")
plt.show()
plt.rc('font', size=14) # 폰트 크기를 다시 키웁니다
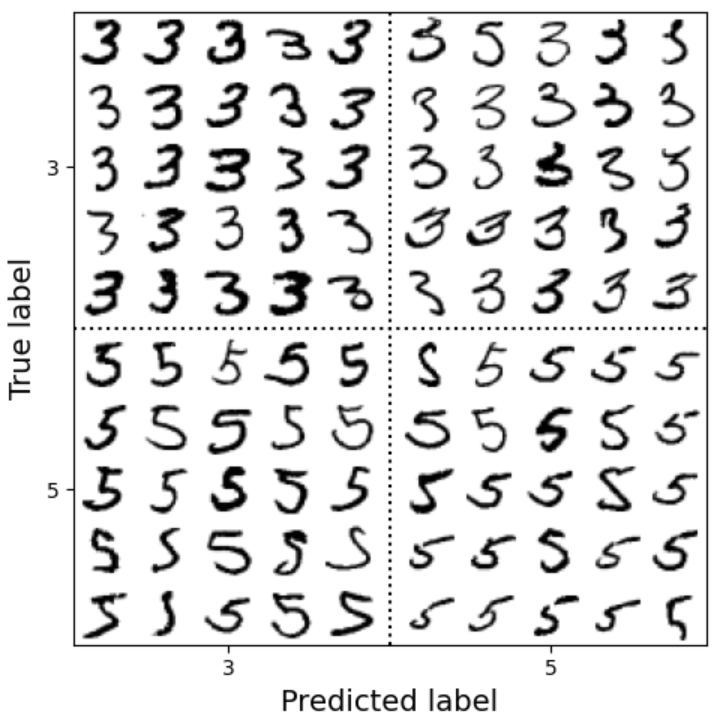
각각의 오류를 분석해보면 분류기가 무슨 일을 하는지, 왜 잘못되었는지 인사이트를 얻을 수 있다. 예를 들어 오차 행렬 스타일로 3과 5의 샘플을 그려보자!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
cl_a, cl_b = '3', '5'
X_aa = X_train[(y_train == cl_a) & (y_train_pred == cl_a)]
X_ab = X_train[(y_train == cl_a) & (y_train_pred == cl_b)]
X_ba = X_train[(y_train == cl_b) & (y_train_pred == cl_a)]
X_bb = X_train[(y_train == cl_b) & (y_train_pred == cl_b)]
# 추가 코드 – 그림 3–11을 생성하고 저장합니다
size = 5
pad = 0.2
plt.figure(figsize=(size, size))
for images, (label_col, label_row) in [(X_ba, (0, 0)), (X_bb, (1, 0)),
(X_aa, (0, 1)), (X_ab, (1, 1))]:
for idx, image_data in enumerate(images[:size*size]):
x = idx % size + label_col * (size + pad)
y = idx // size + label_row * (size + pad)
plt.imshow(image_data.reshape(28, 28), cmap="binary",
extent=(x, x + 1, y, y + 1))
plt.xticks([size / 2, size + pad + size / 2], [str(cl_a), str(cl_b)])
plt.yticks([size / 2, size + pad + size / 2], [str(cl_b), str(cl_a)])
plt.plot([size + pad / 2, size + pad / 2], [0, 2 * size + pad], "k:")
plt.plot([0, 2 * size + pad], [size + pad / 2, size + pad / 2], "k:")
plt.axis([0, 2 * size + pad, 0, 2 * size + pad])
plt.xlabel("Predicted label")
plt.ylabel("True label")
save_fig("error_analysis_digits_plot")
plt.show()
⭐선형 분류기는 클래스마다 픽셀에 가중치를 할당하고 새로운 이미지에 대해 단순히 픽센 강도의 가중치 합을 클래스의 점수로 계산!
⭐모델이 변형에 더 잘 견디도록 데이터 증식이용!
3.6 다중 레이블 분류
🔖다중 레이블 분류?
- 여러 개의 이진 꼬리표를 출력하는 분류 시스템.
🔖KNeighborsClassifier를 이용해 학습시키기!
1
2
3
4
5
6
7
8
9
10
import numpy as np
from sklearn.neighbors import KNeighborsClassifier
y_train_large = (y_train >= '7')
y_train_odd = (y_train.astype('int8') % 2 == 1)
y_multilabel = np.c_[y_train_large, y_train_odd]
# np.c_[] → NumPy에서 여러 개의 1D 배열을 열(column) 기준으로 병합하는 기능
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_multilabel)
🔖F1 점수의 평균 계산하기!(평가)
1
2
3
y_train_knn_pred = cross_val_predict(knn_clf, X_train, y_multilabel, cv=3)
f1_score(y_multilabel, y_train_knn_pred, average="macro")
# 0.9764102655606048
클래스가 불균형하다면, 레이블에 클래스의 지지도(타깃 레이블에 속한 샘플 수)를 가중치로 주자!
1
2
3
# 추가 코드 – average="weighted"로 지정했을 때 성능 향상은 무시할 수 있는 수준입니다.
# 이 클래스는 이미 꽤 균형 잡혀 있기 때문입니다.
f1_score(y_multilabel, y_train_knn_pred, average="weighted")
🔖다중 레이블 분류를 지원하지 않는 분류기 사용?
- 레이블당 하나의 모델을 학습시키자!
- 단, 이 방법은 레이블 간의 의존성을 포착하기 어렵게 할 수 있다. => 해결 위해 모델을 체인으로 구성할 수 있음!
=> 사이킷런의 ClassifierChain클래스 이용!
💡ClassifierChain
o 훈련에는 진짜 레이블을 이용
o 단, cv 하이퍼파라미터를 지정하면 교차 검증을 이용하여 훈련 세트의 모든 샘플에 대해 훈련된 각 모델에서 깨끗한 에측을 얻고, 이러한 예측을 이용해 나중에 체인 안의 모든 모델을 훈련.
1
2
3
4
5
6
7
from sklearn.multioutput import ClassifierChain
chain_clf = ClassifierChain(SVC(), cv=3, random_state=42)
chain_clf.fit(X_train[:2000], y_multilabel[:2000])
chain_clf.predict([some_digit])
# array([[0., 1.]])
3.7 다중 출력 분류
🔖다중 출력 다중 클래스 분류(다중 출력 분류)
- 다중 레이블 분류에서 한 레이블이 다중 클래스가 될 수 있도록 일반화 한것.(값을 두 개 이상 가질 수 O)
🔖이미지에서 잡음을 제거하는 시스템 만들기!
1
2
3
4
5
6
7
np.random.seed(42) # 동일하게 재현되게 하려고 지정합니다
noise = np.random.randint(0, 100, (len(X_train), 784))
X_train_mod = X_train + noise
noise = np.random.randint(0, 100, (len(X_test), 784))
X_test_mod = X_test + noise
y_train_mod = X_train
y_test_mod = X_test
1
2
3
4
5
6
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train_mod, y_train_mod)
clean_digit = knn_clsf.predict([X_test_mod[0]])
plot_digit(clean_digit)
save_fig("cleaned_digit_example_plot") # 추가 코드 – 그림 3–13을 저장합니다
plt.show()