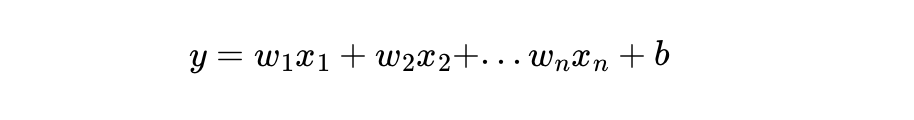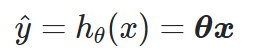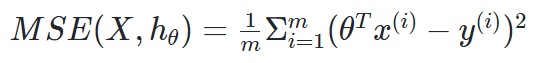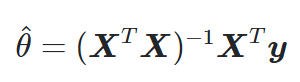4장. 모델 훈련

🔖선형 회귀를 학습시키는 두 가지 방안

1. 닫힌 형태의 방정식을 사용하여 훈련 세트에 가장 잘 맞는 모델 파라미터(즉, 훈련 세트에 대해 비용 함수를 최소화하는 모델 파라미터)를 직접 계산한다.
2. 경사 하강법이라 불리는 반복적인 최적화 방식을 이용하여 모델 파라미터를 조금씩 바꾸면서 비용 함수를 훈련 세트에 대해 최소화시킨다. 결국에는 앞의 방법과 동일한 파라미터로 수렵한다.

4.1 선형 회귀

• y는 예측값
• n은 특성의 수
• xi는 i번째 특성 값
• Wj는 j번째 모델 파라미터
• b는 편향

• h는 모델 파라미터를 사용한 가설 함수
• θ는 편향 θ0와 가중치 θ1, θ2,θ3,…,θn 까지의 특성 가중치를 담은 모델의 파라미터 벡터
• x는 특성 벡터. x0는 항상 1입니다.
• θx: 벡터 θ와 x의 점곱(dot product)

🔖학습

• RMSE나 MSE를 최소화하는 θ찾기

4.1.1 정규 방정식

• 비용 함수를 최소화하는 θ를 찾기위한 해석적 방법에서 이용하는 수학 공식.

import numpy as np

np.random.seed(42)  # 코드 예제를 재현 가능하게 만들기 위해
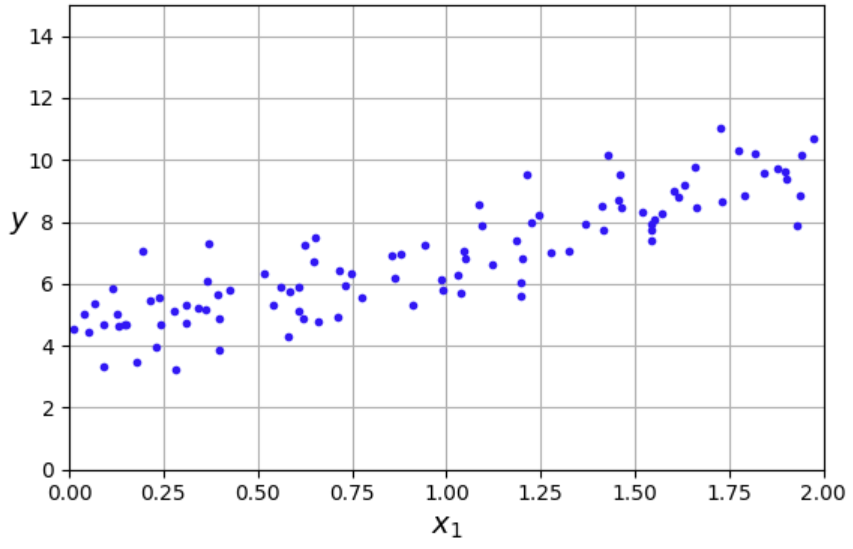
m = 100  # 샘플 개수
X = 2 * np.random.rand(m, 1)  # 열 벡터
y = 4 + 3 * X + np.random.randn(m, 1)  # 열 벡터

🔖정규 방정식을 사용하여 최소화하는 θ구함

from sklearn.preprocessing import add_dummy_feature

X_b = add_dummy_feature(X)  # 각 샘플에 x0 = 1을 추가합니다.
theta_best = np.linalg.inv(X_b.T @ X_b) @ X_b.T @ y
# inv() 함수를 이용해 역행렬을 계산하고 dot() 메서드를 사용해 행렬 곱셈 수행.
# @연산자는 행렬 곱셈을 수행.

theta_best
# array([[4.21509616],
#     [2.77011339]])

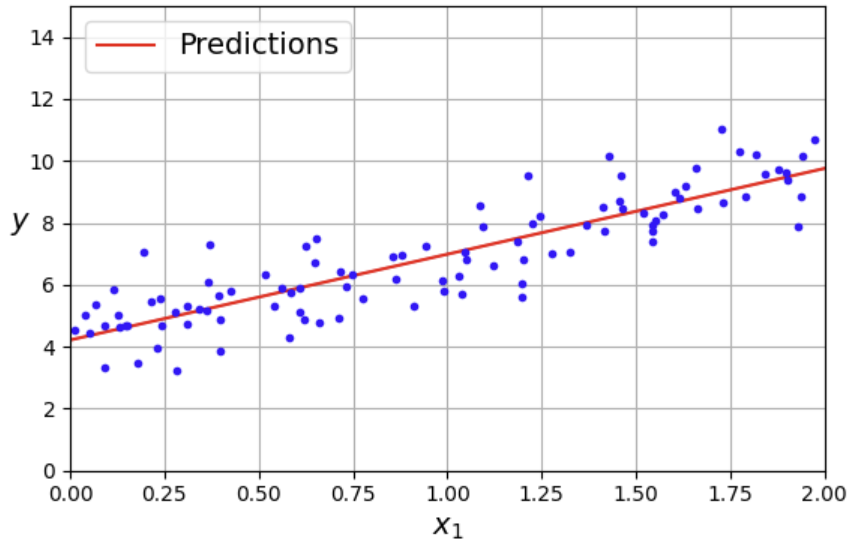
🔖모델 예측 나타내보기

import matplotlib.pyplot as plt

plt.figure(figsize=(6, 4))  # 추가 코드
plt.plot(X_new, y_predict, "r-", label="Predictions")
plt.plot(X, y, "b.")

# 추가 코드 - 그림 4-2를 꾸미고 저장합니다.
plt.xlabel("$x_1$")
plt.ylabel("$y$", rotation=0)
plt.axis([0, 2, 0, 15])
plt.grid()
plt.legend(loc="upper left")
save_fig("linear_model_predictions_plot")

plt.show()

🔖사이킷런에서 선형 회귀 수행

from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(X, y)
lin_reg.intercept_, lin_reg.coef_
# (array([4.21509616]), array([[2.77011339]]))
lin_reg.predict(X_new)
# array([[4.21509616],
#     [9.75532293]])

직접 호출도 가능!

theta_best_svd, residuals, rank, s = np.linalg.lstsq(X_b, y, rcond=1e-6)
theta_best_svd
# array([[4.21509616],
#     [2.77011339]])

이 함수는 $\mathbf{X}^+\mathbf{y}$을 계산합니다. $\mathbf{X}^{+}$는 $\mathbf{X}$의 유사역행렬 (pseudoinverse)입니다(Moore–Penrose 유사역행렬입니다). np.linalg.pinv()을 사용해서 유사역행렬을 직접 계산할 수 있습니다

np.linalg.pinv(X_b) @ y
# array([[4.21509616],
#     [2.77011339]])

유사행렬 자체는 특잇값 분해라 부르는 표준 행렬 분해 기법을 사용해 계산한다. SVD는 훈련 세트 행렬 X를 3개의 행렬 곱셈 U * Sigma * V^T로 분해합니다. 유사역행렬은 X+ = V * Sigma+ * U^T 로 계산됩니다. sigma+를 계산하기 위해 알고리즘이 sigma를 먼저 구한 다음 어떤 낮은 임곗값보다 작은 모든 수를 0으로 바꿉니다. 그다음 0이 아닌 모든 값을 역수로 치환한다. 마지막으로 만들어진 행렬을 전치한다. 정규 방정식을 계산하는 것보다 이 방식이 훨씬 효율적이다. 또한 극단적인 경우도 처리할 수 있다.

❗m < n이거나 어떤 특성이 중복되어 행렬 $\mathbf{X}^t\mathbf{X}$의 역행렬이 없다면(즉, 특이 행렬이라면) 정규 방정식이 작동하지 않는다. 하지만 유사역행렬은 항상 구할 수 있다.

4.1.2 계산 복잡도