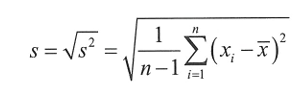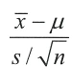4장.추론통계~신뢰구간

4.1 추론통계를 배우기 전에

전수조사와 표본조사

모집단을 알아보는 방법

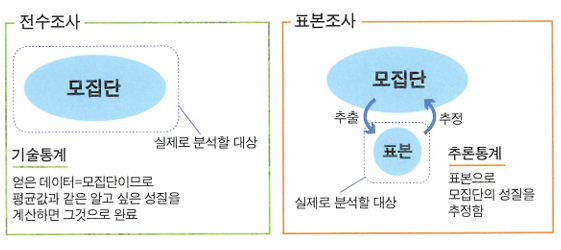
🔖전수조사

• 모집단의 모든 요소 조사

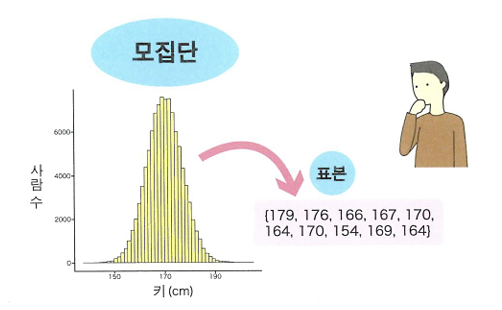
🔖표본조사

• 모집단의 일부인 표본으로 모집단의 성질을 추정

데이터를 얻는다는 것

• 모집단 분포: 모집단을 나타내는 분포
  • 모집단 분포가 양적 변수의 분포라면 평균이나 분산을 정의할 수 있는데, 이를 각각 모평균, 모분산이라고 한다.
  • 모집단분포를 특징 짓는 양을 모수 또는 파라미터라고 부른다.

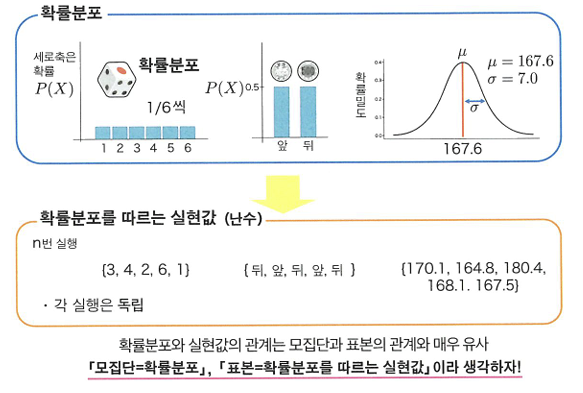
🔖확률분포와 실현값

• 실현값이 마치 데이터처럼 보인다.
• 확률 분포와 실현값의 관계는 모집단과 표본의 관계와 매우 비슷하다.

🔖데이터로부터 그 발생원의 확률분포 추정하기

• 얻은 표본으로 모집단을 추정한다 = 얻은 실현값으로 이 값을 발생시킨 확률분포를 추정한다

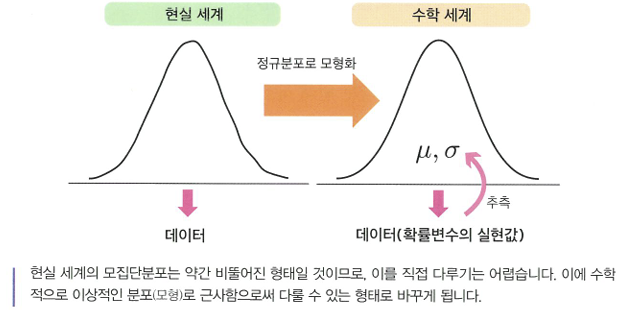
🔖모집단분포 모형화

• 모형화: 수학적인 확률분포로 모집단분포를 근사하는 것.

🔖무작위추출

• 무작위추출: 데이터를 얻을 때 모집단에 포함된 요소를 하나씩 무작위로 선택하여 추출하는 방식.

🔖무작위추출 방법

• 단순무작위추출법: 난수를 이용하여 표본 정함
• 층화추출법: 모집단을 몇 개의 층으로 미리 나눈 뒤, 각 층에서 필요한 수의 조사대상을 무작위로 추출하는 방법.
• 계통추출법
• 군집추출법

🔖편향된 추출로는 올바른 추정이 어려움

• 편향된 추출로써 표본을 만든 경우라면, 표본으로 모집단을 올바르게 추정할 수 없다.

🔖데이터 얻는 법

• 모집단에 대해 추정한 결과를 어느 정도 일반화할 수 있는가는, 각 분야 고유이 지식에 따라 달라집니다.

추론통계를 직감적으로 이해하기

• 시사점
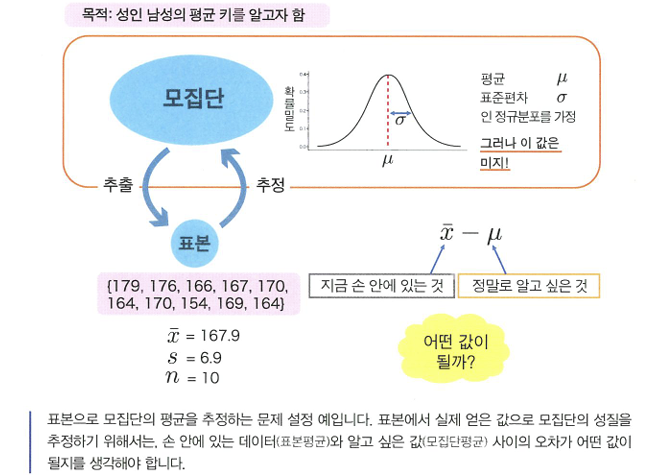
  • 정말 알고자 하는 것은 표본데이터x 모집단
  • 모집단의 모든 요소를 다 조사하는 전수조사는 어렵다.
  • 작은 크기의 표본으로도 모집단을 추론할 수 있다.
  • 표본을 추출할 때는 무작위로 추출해야 한다.

4.2 표본오차와 신뢰구간

모집단과 데이터 사이의 오차 고려하기

표본오차

• 표본오차: “정말로 알고 싶은 것”과 “실제로 손 안에 있는 데이터”에 발생하는 오차(평균에만 국한x)

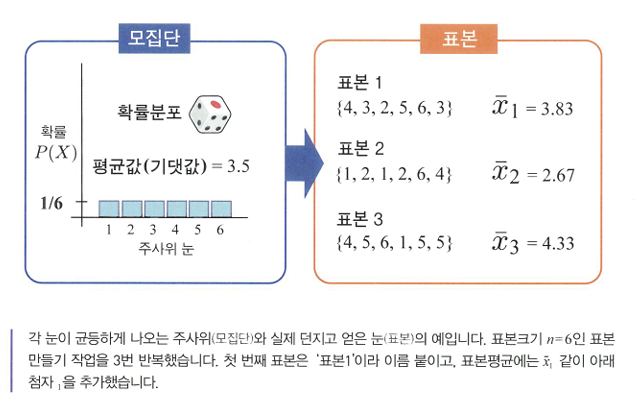
🔖주사위의 표본오차

🔖표본오차는 확률적으로 바뀐다.

• 표본은 모집단의 성질과 정확히 일치하지 않고, 확률오차를 수반한다.

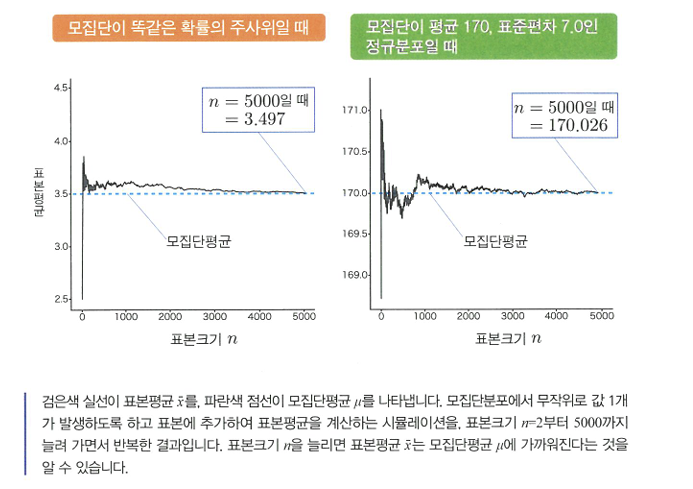
🔖큰 수의 법칙

• 큰수의 법칙: 표본크기 n이 커질수록 표본평균이 모집단평균에 한없이 가까워진다는 법칙

표본오차의 확률분포

• 표본오차의 확률분포를 알면 어느 정도 크기의 오차가, 어느 정도의 확률로 나타나는지를 알 수 있게 된다.

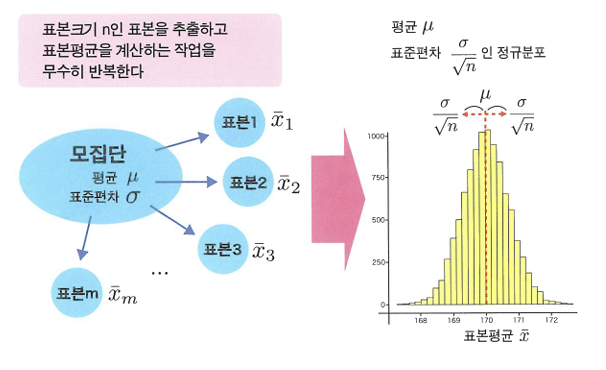
🔖중심극한정리

• 중심극한정리: 모집단이 어떤 분포이든 간에, 표본크기 n이 커질수록 표본평균 x의 분포는 정규분포로 근사할 수 있다.

🔖추정량

• 추정량: 모집단의 성질을 추정하는데 이용하는 통계량(확률 변수)
• 일치추정량: 표본크기 n을 무한대로 했을 때, 모집단의 성질과 일치하는 추정량
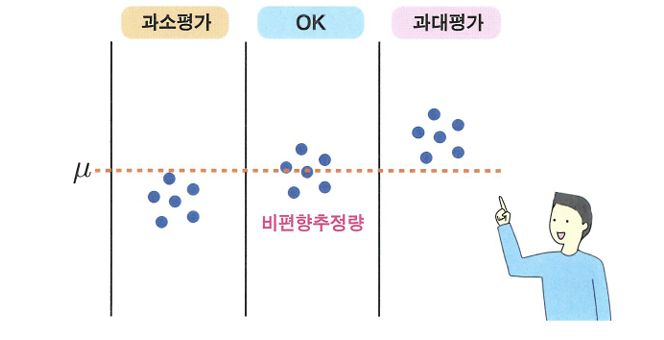
• 비편향추정량: 추정량의 평균값이 모집단의 성질과 일치할 때
  • 매번 얻을 때마다 확률적으로 다른 값이 되지만, 평균으로 보면 보집단의 성질을 과대하지도 과소하지도 않게 나타내는 양을 뜻한다.(표본평균 = 비편향추정량)

⭐모집단 표준편차의 비편향추정량

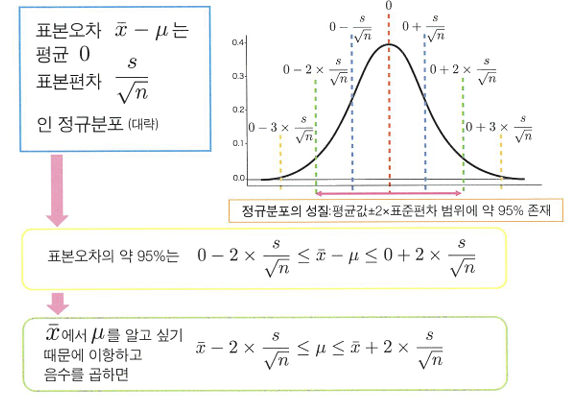
🔖표준오차의 분포

• 이때 모집단의 표준편차를 모르기에 표본에서 추정한 비편향표준편차 s를 대신 사용한다.

신뢰구간이란?

• 신뢰구간: 표본에서 구한 모집단 u의 추정값을 어느 정도 신뢰할 수 있는지 나타내는 값.

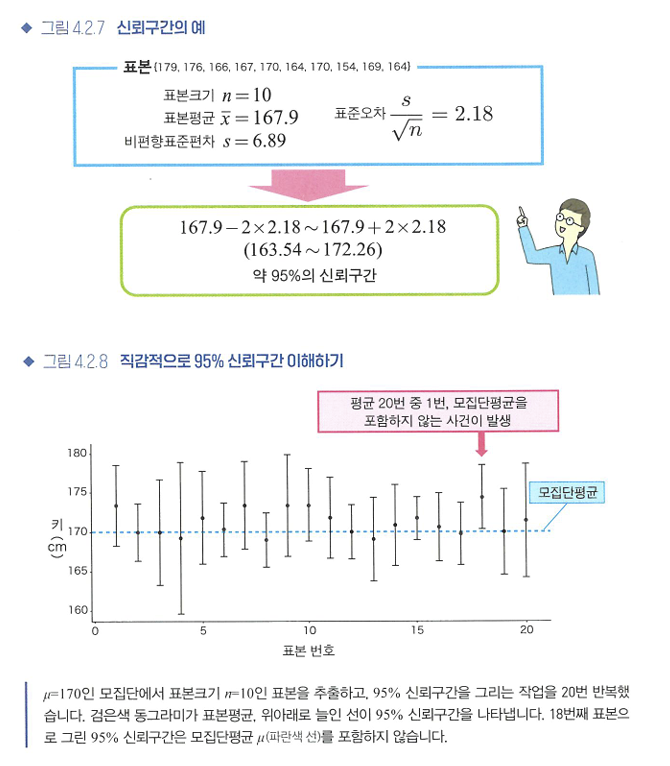
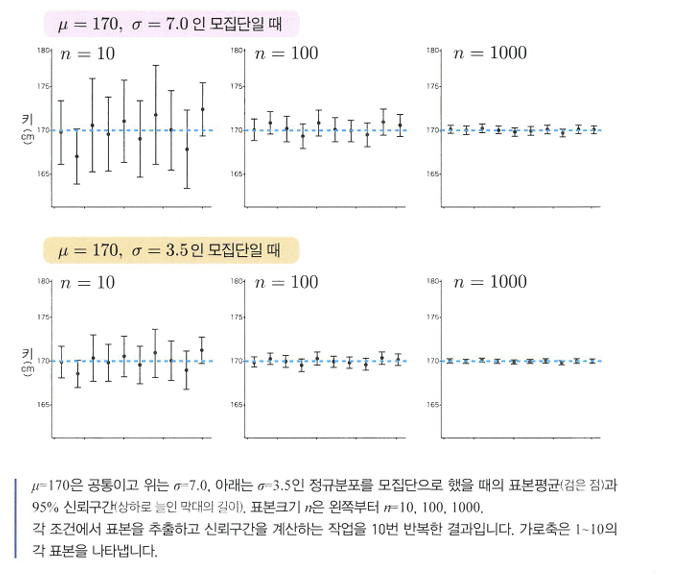
🔖신뢰구간의 해석

• oo%의 신뢰구간: oo%의 확률로 이 구간에 모집단평균이 있다.
  • 모집단평균이 확률적으로 변하여 그 구간에 포함되는게 아니라, 모집단에서 표본을 추출하여 oo% 신뢰구간을 구하는 작업을 100번 반복했을때 평균적으로 그 구간에 u가 포함되는 것이 oo번이란 뜻.

🔖신뢰구간의 구체적인 예

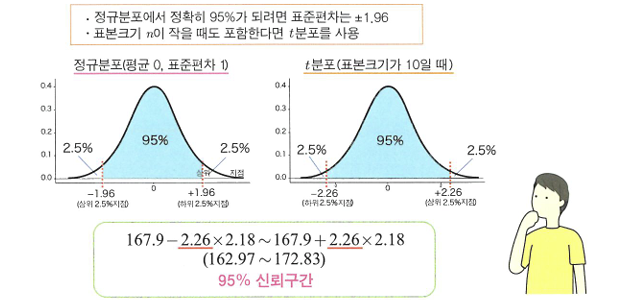
t분포와 95% 신뢰구간

• t 분포: 모집단이 정규분포라는 가정하에 미지의 모집단 표준편차를 표본으로 계산한 비편향표준편차 s로 대응했을 때, x-u를 표준오차로 나누어 표준화한 값이 따르는 분포.

🔖정밀도를 높이려면

• 표준오차⬇️
  • 비편향표준오차 줄이기
  • 표본크기 n 줄이기

🔖t분포를 사용할 때 주의할 점

• 정규분포에서 얻은 데이터라는 가정 필요.(단, 표본크기가 클 때는 중심극한정리에 따라 모집단이 정규분포가 아니더라도 표본평균을 정규분포로 근사할 수 있으므로 신뢰구간은 확실해짐.)