5장.가설검정

5.1 가설검정의 원리

또 하나의 추론통계 방법

• 가설검정: 분석자가 세운 가설을 검증하기 위한 방법.
  • p값이라는 수치를 계산하여 가설을 지지하는지 여부를 판단합니다.

🔖가설 검증하기

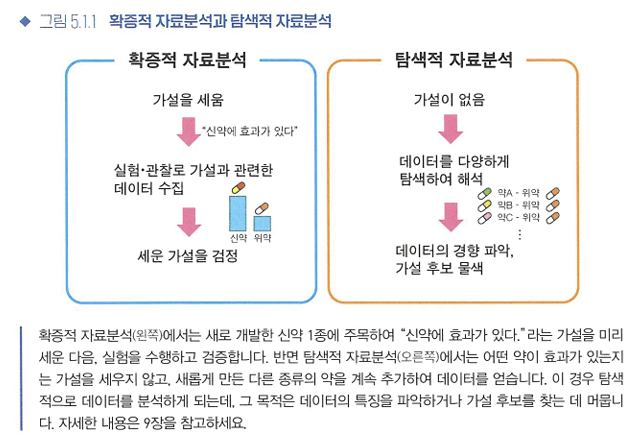
• 확증적 자료분석: 미리 세운 가설을 검증하는 접근법
• 탐색적 자료분석: 전체 데이터를 탐색적으로 해석하는 접근법
  • 데이터의 특징이나 경향 파악
  • 가설 후보를 찾는 것을 목적으로 함

🔖가설검정

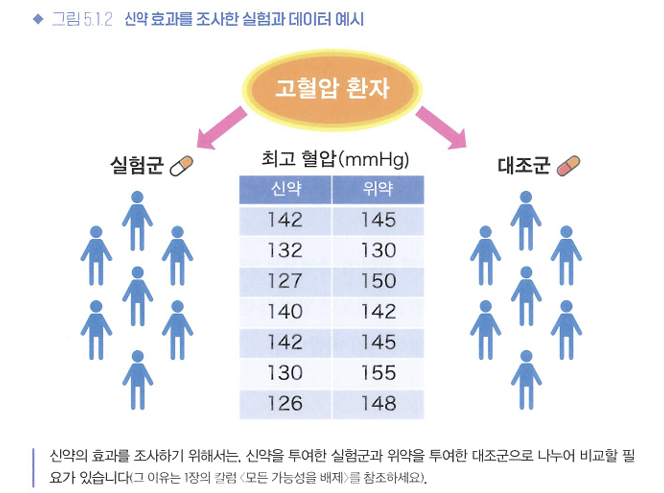
• 군: 특정 동일 조건인 집단
  • 실험군: 어떤 조치를 취한 집단
  • 대조군: 실험군과 비교/대조를 위해 마련한 집단

통계학에서 가설이란?

❗세운 가설은 모집단을 대상으로 한 가설!

🔖귀무가설과 대립가설

❗대립가설을 부정하여 귀무가설을 지지하는 것은 불가능!

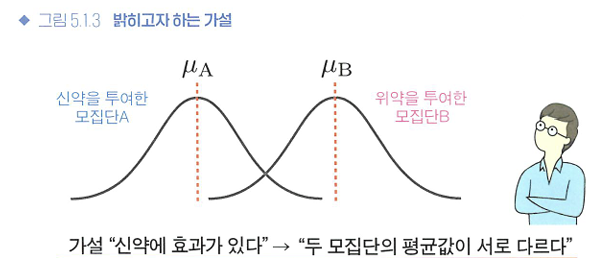
• 귀무가설: 밝히고자 하는 가설의 부정 명제
• 대립가설: 밝히고 싶은 가설
  => 가설검정에서는 상정한 가설을 확인하고자 그 부정 명제인 귀무가설을 세우고, 이 귀무가설이 틀렸음을 주장하는 것으로 대립가설을 지지한다는 흐름.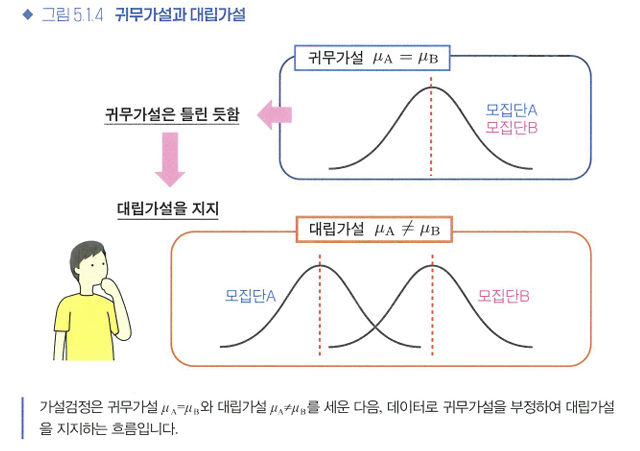

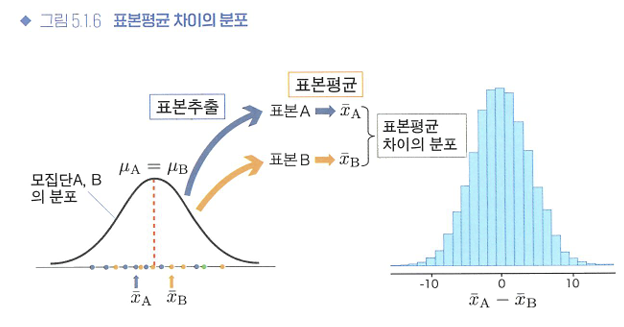
🔖모집단과 표본의 관계 다시 살펴보기

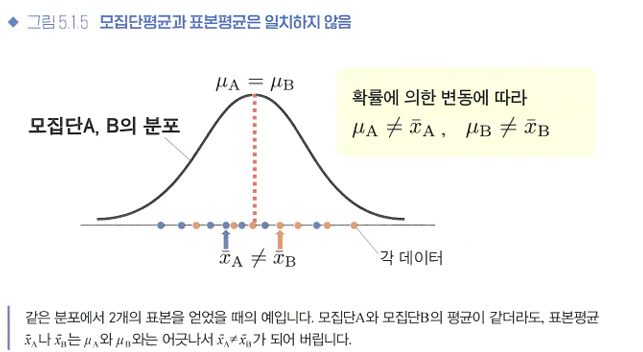
표본평균의 차이가 귀무가설이 옳을 때도 생기는 단순한 데이터 퍼짐인지, 아니면 정말로 약의 효과인지를 구별할 필요가 있다.

🔖귀무가설이 옳은 세계 상상하기

⭐귀무가설이 옳을 때도 생기는 단순한 데이터 퍼짐에서 비롯된 차이인지, 아니면 정말로 약의 효과인지를 구별하여, 귀무가설이 틀렸는지를 조사하는 과정!

1. 귀무가설이 옳다고 가정한다.
2. 모집단 A와 모집단 B에서 각각 표본을 추출한다.
3. 이 작업을 여러 번 반복하고, 표본평균의 차이를 히스토그램으로 그려본다.(귀무가설이 옳은 세계에서 표본평균의 차이가 확률적으로 어떻게 생기는지를 나타내는 분포)

=> 표본평균 차이는 평균적으로 0, 0에 가까운 값이 나타나기 쉽고, +10과 같이 큰 값이나 -10과 같이 작은 값은 비교적 나타나기 어렵다.

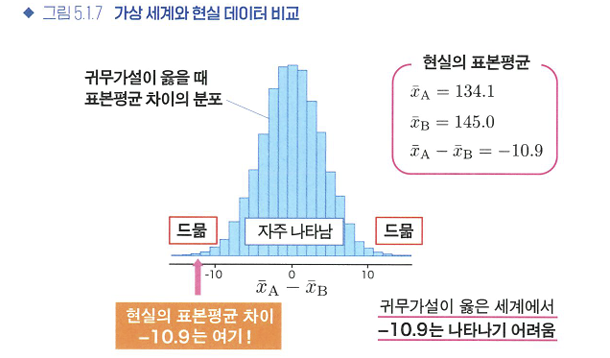
P값

❓ 현실의 값은 귀무가설이 옳은 가상 세계에서는 어떤 빈도로 발생할까?

• P값: 현실에서 얻은 데이터가 귀무가설이 옳은 가상 세계에서는 얼마나 나타나기 쉬운가, 또는 어려운가를 평가하고자 도입된 값.
  • 0이상 1이하(확률)

🔖P값과 유의수준 a를 이용한 가설 판정

1. 통계적으로 유의미한 차이가 있다.
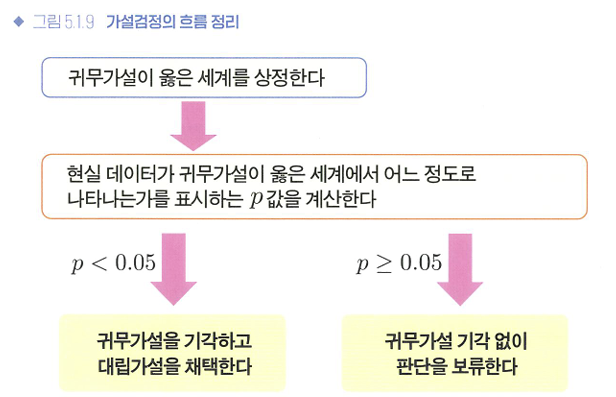
   • p값이 0.05 이하인 경우
     • 귀무가설 하에서 현실 데이터는 나타나기 어렵다.
     • 귀무가설을 버리고 대립가설을 체택!
2. 통계적으로 유의미한 차이는 발견하지 못했다.
   • p값이 0.05를 상회하는 경우
     • 귀무가설을 기각할 수 없다.

• 유의수준 a: 귀무가설을 기각할 것인지 체택할 것인지의 판단 경계로 이용하는 값

가설검정 흐름 정리

5.2 가설검정 시행

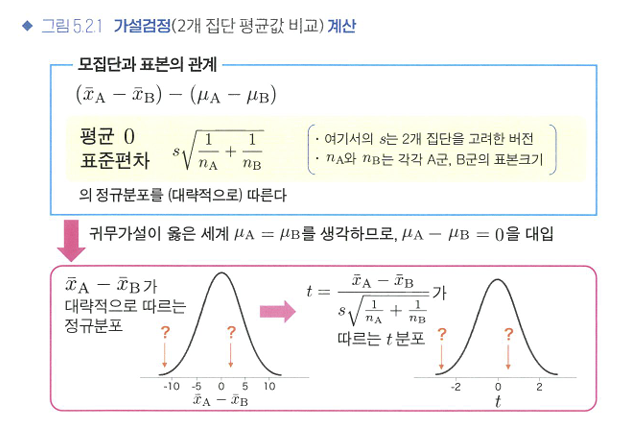
가설검정의 구체적인 계산

❗가설검정의 개념은 다양한 검정기법에서 공통이지만, p값의 계산 방법은 서로 다릅니다.

• 이표본 t검정: 2개 집단 간의 평균값을 비교하는 검정

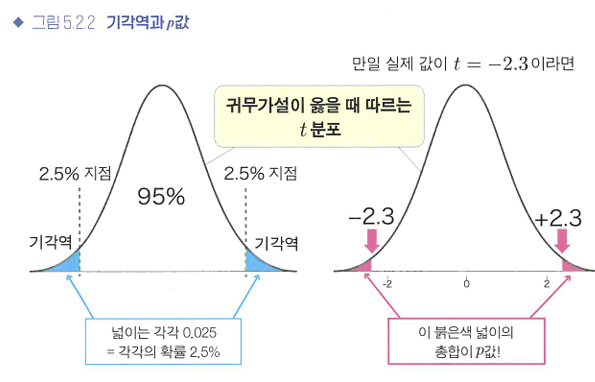
기각역과 p값

• 기각역: 좌우 2.5%씩의 영역을 유의수준 5%인 기각역이라고 한다.
  • 실제로 얻은 값이 기각역에 포함될 때는 p<0.05가 되며, 귀무가설 기각!

• p값: 실제 값이 이 귀무가설이 옳을 때의 t분포 내 어디에 위치하는지 구한 뒤, 그 이상의 극단적인 값이 나올 확률을 구한 값.

• 양측검정: 양수와 음수 양쪽을 모두 고려
• 단측검정: 어느 한쪽만 고려

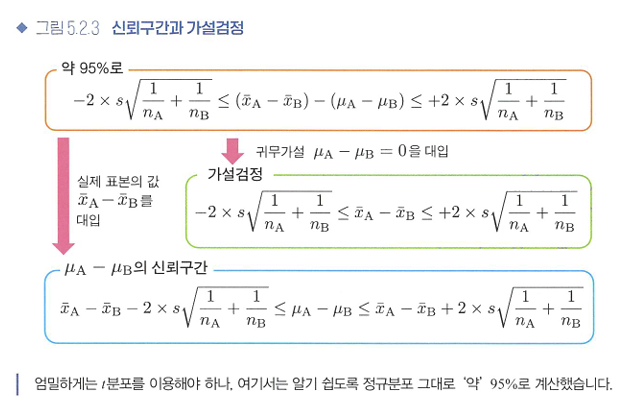
실뢰구간과 가설검정의 관계

• 실제 값인 표본평균으로 모집단평균을 추정하는 것이 신뢰구간이며, 귀무가설을 가정해 모집단평균을 0으로 고정했을 때의 표본평균이 어떤 값이 될 것인지를 구하는 것이 가설검정.
  => 표본평균 차이의 95% 신뢰구간이 0에 걸치는지 여부와, p값이 0.05를 밑도는지 여부는 등치!

가설검정의 구체적인 예

5.3 가설검정 관련 그래프

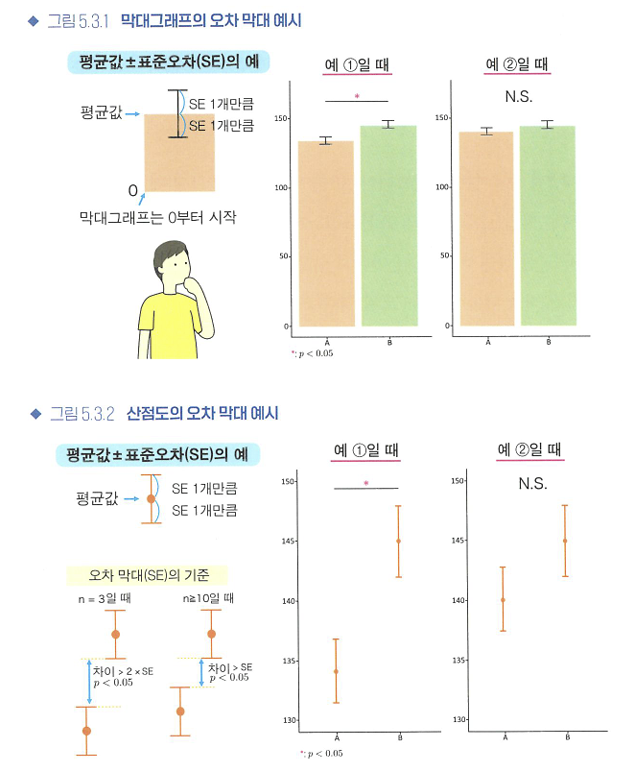
오차 막대

• 오차 막대: 반복이 있는 데이터에서 평균값을 계산하여 막대그래프나 산점도로 그릴 때는, 평균값에 더하여 그 위아래로 오차 막대를 함께 그린다.

“통계적으로 유의미”를 나타내는 표기

• *: 0.01 <= p < 0.05
• **: 0.001 <= p < 0.01
• ***: p < 0.001
• N.S: 유의미x

5.4 제 1종 오류와 제 2종 오류

진실과 판단의 4패턴

🔖제 1종 오류

• 제 1종 오류: 실제로는 아무런 차이가 없음에도 차이가 있다고 판단해 버리는 잘못.
• p 값과 유의수준 a를 이용하여 제 1종 오류가 일어날 확률을 통제할 수 있다.
  • 귀무가설이 옳은데도 착오로 귀무가설을 기각해 버리는 오류가 확률 a로 발생! => a 통제하면 1종 오류 통제 가능

🔖제 2종 오류

• 제 2종 오류: 정말로 차이가 있는데도 차이가 있다고는 말할 수 없어, 귀무 가설을 기각하지 않는 판단을 내려 버리는 것.
• 검정력(1-B): 정말로 차이가 있을 때 차이가 있다고 올바르게 판단할 확률
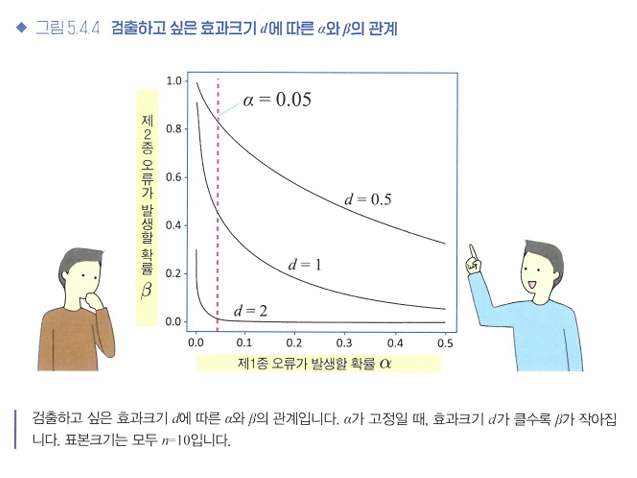
  • B는 직접 통제x n이 커질수록 작아지며, 어느 정도의 차이를 차이로 간주하는지를 나타내는 값인 효과크기가 커짐에 따라서도 작아집니다.

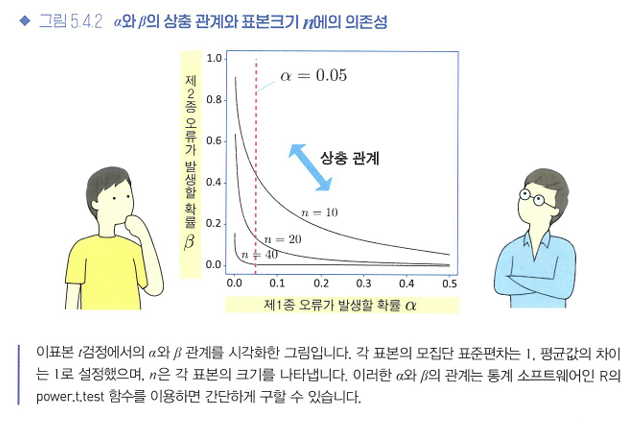
a와 B는 상충 관계

• a와 B사이에는 상충 관계 , 즉 한쪽이 작아지면 한쪽은 커지는 관계가 있습니다.
  • 이 관계는 n에 따라 달라진다.

효과크기를 달리 했을 때의 a와 B

• 효과크기: 얼마나 큰 효과가 있는지를 나타내는 지표

a와 B, 표본크기 n, 효과크기 d의 네 값 중 셋을 설정하면, 나머지 하나는 자동으로 정해진다.