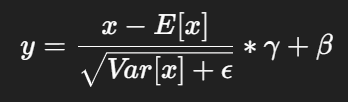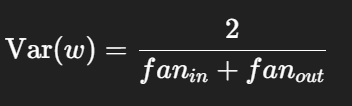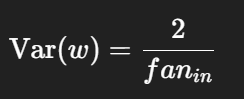[5 2] resnet 구현

Q1. Batch Normalization 외 다른 Normalization 방법?

1. LayerNorm

LayerNorm

class torch.nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True, bias=True, device=None, dtype=None)

🧩 Layer Normalization (층 정규화)

• Layer Normalization은 입력 미니배치에 대해 정규화를 적용하는 층이야. 즉, 각 샘플(한 배치 안의 한 데이터)에 대해 평균과 분산을 구해 정규화해 주는 방식이야.

⚙️ 수식

• E[x] : 입력의 평균
• Var[x] : 입력의 분산
• ε (epsilon) : 0으로 나누는 것을 방지하기 위한 작은 상수
• γ (gamma) : 학습 가능한 스케일(가중치)
• β (beta) : 학습 가능한 시프트(편향)

정규화 범위

• normalized_shape에 따라 정규화되는 차원이 결정돼.
  • 예를 들어, normalized_shape = (3, 5) 라면 입력 텐서의 마지막 두 차원(-2, -1) 을 기준으로 평균과 분산을 계산해. 즉, input.mean((-2, -1)) 과 같은 연산이 일어나는 거야.

🧠 학습 가능한 파라미터 (γ, β)

• elementwise_affine=True일 경우, γ와 β는 학습 가능한 파라미터가 돼.
• 이때 γ와 β의 크기는 normalized_shape와 동일하고,
  • γ는 1로 초기화되고
  • β는 0으로 초기화돼.
  • 이들은 각 요소(element) 마다 별도로 적용되는 per-element scale, bias야.

🧮 분산 계산

분산은 biased estimator (편향된 추정기)로 계산돼. 즉, torch.var(input, unbiased=False) 와 동일한 방식으로 수행돼

💡 BatchNorm / InstanceNorm 과의 차이점

구분	정규화 범위	학습 파라미터
Batch Normalization	배치 전체	채널 단위
Instance Normalization	각 샘플의 채널별	채널 단위
Layer Normalization	각 샘플의 모든 feature	요소 단위

예시

# NLP Example
batch, sentence_length, embedding_dim = 20, 5, 10
embedding = torch.randn(batch, sentence_length, embedding_dim)
layer_norm = nn.LayerNorm(embedding_dim)
# Activate module
layer_norm(embedding)
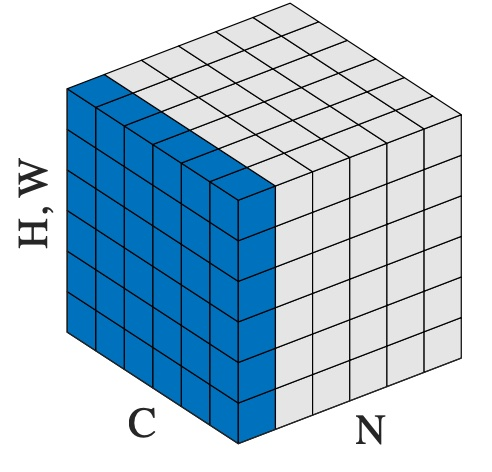
# Image Example
N, C, H, W = 20, 5, 10, 10
input = torch.randn(N, C, H, W)
# Normalize over the last three dimensions (i.e. the channel and spatial dimensions)
# as shown in the image below
layer_norm = nn.LayerNorm([C, H, W])
output = layer_norm(input)

or

nn.GroupNorm(1, out_channels)

2. GroupNorm

🧩 1️⃣ 기본 개념

Group Normalization (GN) 은 입력의 채널을 여러 “그룹”으로 나눠서, 각 그룹 안에서 평균과 분산을 계산해 정규화하는 방법이야.

수식은 LayerNorm과 거의 같아. 단, 평균 E[x]와 분산 Var[x]을 “각 그룹별로” 계산한다는 게 핵심 차이야.

⚙️ 2️⃣ 어떻게 그룹을 나누는가?

입력 텐서의 shape:

(N, C, H, W)

• N: 배치 크기 (정규화 계산에는 포함 안 됨)
• C: 채널 수 (예: 64)
• H, W: 공간 차원 (이미지의 높이, 너비)

num_groups	그룹 구성	정규화 범위
1	모든 채널이 한 그룹	LayerNorm과 동일
C	각 채널이 한 그룹	InstanceNorm과 동일
중간 값(예: 32, 8 등)	C를 num_groups로 나눔	GN 고유 형태

🧮 3️⃣ 예시로 보기

• 예를 들어 입력이 (N=2, C=8, H=4, W=4)이고, num_groups=4라면:
  • 총 8채널을 4개 그룹으로 나눔 → 그룹당 2채널씩
  • 각 그룹 안의 (2 x 4 x 4) 값들로 평균과 분산 계산
  • 그걸로 정규화

  즉, 각 그룹이 독립적으로 평균 0, 분산 1로 맞춰지는 거야.

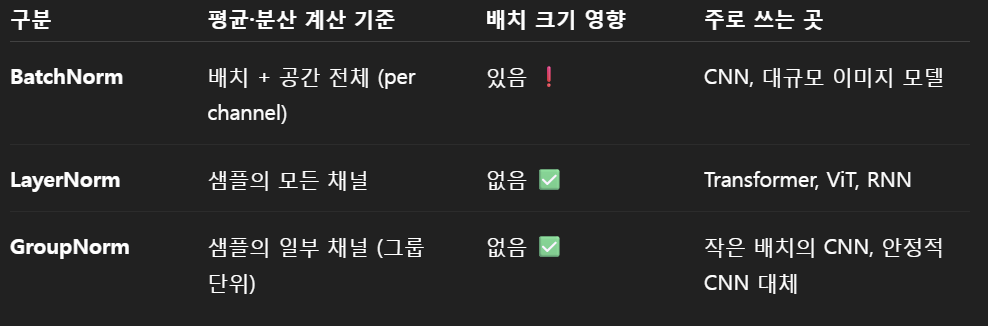
📊 4️⃣ BatchNorm / LayerNorm / GroupNorm 비교

3. InstanceNorm

• GroupNorm의 C를 C로 한것!
• 즉 한 sample 당 하나의 channel을 기준으로 정규화

4. RMS(제곱평균제곱근)

핵심 요약

• 수식
  • 평균을 빼지 않고 표준편차 대신 RMS로만 스케일링
  • γ만 있음(기본적으로 bias/β 없음)
• 정규화 축: normalized_shape의 마지막 D개 차원(=LayerNorm과 동일한 축 선택 방식)
• 장점: 계산 단순(빠름), 안정적, 대형 Transformer/LLM에서 자주 사용(LLaMA류 등)

언제 쓰니?

• Transformer/ViT/MLP 블록의 hidden 차원 정규화에 아주 흔함: nn.RMSNorm(hidden_dim)
• CNN(NCHW)에서는 드뭄(대신 BN/GN/LN 더 흔함). 그래도 쓰려면 축을 맞춰줘야 함(아래 코드 참고).

normalized_shape 이해 (입력 (N, H, W, C) & (N, C, H, W))

• 입력이 (N, *, D)꼴이면 보통 normalized_shape=(D,)로 마지막 차원 기준 정규화
• 예: Transformer 입력 (N, seq_len, hidden_dim) → RMSNorm(hidden_dim)
• 이미지는 PyTorch가 기본 NCHW이므로, 마지막 차원이 채널이 아니기 때문에 바로 쓰면 의도와 다름 → 간단한 래퍼로 NHWC로 바꿔 적용하면 돼

class RMSNorm2d(nn.Module):
    def __init__(self, num_channels, eps=None, elementwise_affine=True):
        super().__init__()
        self.norm = nn.RMSNorm(normalized_shape=num_channels, eps=eps, elementwise_affine=elementwise_affine)

    def forward(self, x):          
        x = x.permute(0, 2, 3, 1)  
        x = self.norm(x)          
        x = x.permute(0, 3, 1, 2)  
        return x
      
# Resnet 블록에서..
self.residual_function = nn.Sequential(
    nn.Conv2d(in_channels, out_channels, kernel_size=3, stride=stride, padding=1, bias=False),
    RMSNorm2d(out_channels),   
    nn.ReLU(inplace=True),
    nn.Conv2d(out_channels, out_channels, kernel_size=3, stride=1, padding=1, bias=False),
    RMSNorm2d(out_channels),   
)

...
if stride != 1 or in_channels != out_channels:
    self.shortcut = nn.Sequential(
        nn.Conv2d(in_channels, out_channels, kernel_size=1, stride=stride, bias=False),
        RMSNorm2d(out_channels),  
    )

Q2. ResNet32 구현

import torch
import torch.nn as nn
import torchvision
import torchvision.transforms as transforms

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
CIFAR10_MEAN = (0.4914, 0.4822, 0.4465)
CIFAR10_STD  = (0.2470, 0.2435, 0.2616)
num_epochs = 80
learning_rate = 0.001

transform = transforms.Compose([
    transforms.Pad(4),
    transforms.RandomHorizontalFlip(),
    transforms.RandomCrop(32),
    transforms.ToTensor(),
    transforms.Normalize(CIFAR10_MEAN, CIFAR10_STD),
])
test_transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize(CIFAR10_MEAN, CIFAR10_STD),   # ← 테스트에도
])

train_dataset = torchvision.datasets.CIFAR10(root='../../data/',
                                             train = True,
                                             transform=transform,
                                             download = True)
test_dataset = torchvision.datasets.CIFAR10(root='../../data/',
                                            train = False,
                                            transform = test_transform)

train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
                                           batch_size = 100,
                                           shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset = test_dataset,
                                          batch_size=100,
                                          shuffle=False)


# Basic block
class BasicBlock(nn.Module):
  def __init__(self, in_channels, out_channels, stride = 1):
    super().__init__()

    self.residual_function = nn.Sequential(
        nn.Conv2d(in_channels, out_channels, kernel_size=3, stride=stride, padding=1,bias=False),
        nn.BatchNorm2d(out_channels), #layernorm일땐 nn.GroupNorm(1, out_channels) / Groupnorm일땐 nn.GroupNorm(32, out_channels) / instancenorm 일때 nn.GroupNorm(out_channels, out_channels)
        nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=3, stride=1, padding=1, bias=False),
        nn.BatchNorm2d(out_channels),
    )

    self.shortcut = nn.Sequential()

    if stride != 1 or in_channels != out_channels:
      self.shortcut = nn.Sequential(
          nn.Conv2d(in_channels, out_channels, kernel_size=1, stride = stride, bias = False),
          nn.BatchNorm2d(out_channels),
      )
    
    self.relu = nn.ReLU()
  
  def forward(self, x):
    x = self.residual_function(x) + self.shortcut(x)
    x = self.relu(x)
    return x

class ResNet(nn.Module):
  def __init__(self, block, num_block, num_classes = 10, init_weight = True):
    super().__init__()

    self.in_channels = 64

    self.conv1 = nn.Sequential(
        nn.Conv2d(3, 64, kernel_size = 7, stride = 2, padding = 3, bias = False),
        nn.BatchNorm2d(64),
        nn.ReLU(),
        nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
    )

    self.conv2_x = self._make_layer(block, 64, num_block[0], 1)
    self.conv3_x = self._make_layer(block, 128, num_block[1], 2)
    self.conv4_x = self._make_layer(block, 256, num_block[2], 2)
    self.conv5_x = self._make_layer(block, 512, num_block[3], 2)

    self.avg_pool = nn.AdaptiveAvgPool2d((1,1))
    self.fc = nn.Linear(512, num_classes)
  
  def _make_layer(self, block, out_channels, num_blocks, stride):
    strides = [stride] + [1] * (num_blocks - 1)
    layers = []
    for stride in strides:
      layers.append(block(self.in_channels, out_channels, stride))
      self.in_channels = out_channels
    
    return nn.Sequential(*layers)
  
  def forward(self, x):
    output = self.conv1(x)
    output = self.conv2_x(output)
    x = self.conv3_x(output)
    x = self.conv4_x(x)
    x = self.conv5_x(x)
    x = self.avg_pool(x)
    x = x.view(x.size(0), -1)
    x = self.fc(x)
    return x

model = ResNet(BasicBlock, [3,4,6,3]).to(device)

criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.AdamW(model.parameters(), lr=learning_rate)

def update_lr(optimizer, lr):
  for param_group in optimizer.param_groups:
    param_group['lr'] = lr

total_step = len(train_loader)
curr_lr = learning_rate

model.train()
for epoch in range(num_epochs):
  for i, (images, labels) in enumerate(train_loader):
    images = images.to(device)
    labels = labels.to(device)
    outputs = model(images)
    loss = criterion(outputs, labels)

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    if (i+1) % 100 == 0:
      print("Epoch [{}/{}], step [{}/{}], Loss: {:4f}".format(epoch+1, num_epochs, i+1, total_step, loss.item()))

  if (epoch+1) % 20 == 0:
    curr_lr /= 3
    update_lr(optimizer, curr_lr)

model.eval()
with torch.no_grad():
  correct = 0
  total = 0
  for images, labels in test_loader:
    images = images.to(device)
    labels = labels.to(device)
    outputs = model(images)
    _, predicted = torch.max(outputs.data, 1)
    total += labels.size(0)
    correct += (predicted == labels).sum().item()

  print('Accuracy of the odel on the test images: {} %'.format(100*correct/total))

Q3. BottleNeck 이용

• 50층 이상의 ResNet은 매개변수 사용 최소화 위해 이용
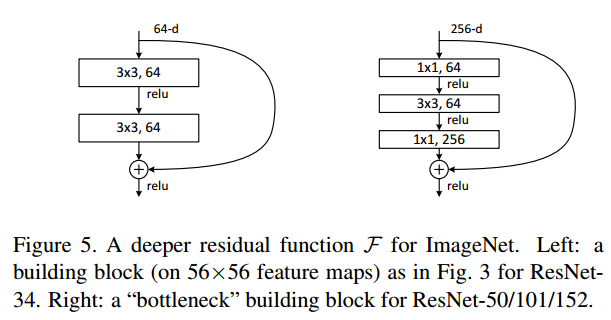
• BottleNeck: Conv 1x1을 이용하여 채널 차원 축소 후 Conv3x3을 이용 -> 다시 Conv1x1로 채널 차원을 복원하는 방식으로 동작하는 block
• 참고: [논문 구현]pytorch로 ResNet(2015) 구현하고 학습하기

Bottleneck Design

신경망이 깊어지면 학습하는데 소요되는 시간은 엄청 오래 걸릴 것 입니다. bottleneck design은 다음과 같이 신경망의 복잡도를 감소하기 위해 사용됩니다.

• NIN과 GoogLeNet에서 제안
• 1x1 conv는 신경망의 성능을 감소시키지 않고 파라미터 수를 감소시킵니다.

Code

github.com/weiaicunzai/pytorch-cifar100

"""resnet in pytorch



[1] Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun.

    Deep Residual Learning for Image Recognition
    https://arxiv.org/abs/1512.03385v1
"""

import torch
import torch.nn as nn

class BasicBlock(nn.Module):
    """Basic Block for resnet 18 and resnet 34

    """

    #BasicBlock and BottleNeck block
    #have different output size
    #we use class attribute expansion
    #to distinct
    expansion = 1

    def __init__(self, in_channels, out_channels, stride=1):
        super().__init__()

        #residual function
        self.residual_function = nn.Sequential(
            nn.Conv2d(in_channels, out_channels, kernel_size=3, stride=stride, padding=1, bias=False),
            nn.BatchNorm2d(out_channels),
            nn.ReLU(inplace=True),
            nn.Conv2d(out_channels, out_channels * BasicBlock.expansion, kernel_size=3, padding=1, bias=False),
            nn.BatchNorm2d(out_channels * BasicBlock.expansion)
        )

        #shortcut
        self.shortcut = nn.Sequential()

        #the shortcut output dimension is not the same with residual function
        #use 1*1 convolution to match the dimension
        if stride != 1 or in_channels != BasicBlock.expansion * out_channels:
            self.shortcut = nn.Sequential(
                nn.Conv2d(in_channels, out_channels * BasicBlock.expansion, kernel_size=1, stride=stride, bias=False),
                nn.BatchNorm2d(out_channels * BasicBlock.expansion)
            )

    def forward(self, x):
        return nn.ReLU(inplace=True)(self.residual_function(x) + self.shortcut(x))

class BottleNeck(nn.Module):
    """Residual block for resnet over 50 layers

    """
    expansion = 4
    def __init__(self, in_channels, out_channels, stride=1):
        super().__init__()
        self.residual_function = nn.Sequential(
            nn.Conv2d(in_channels, out_channels, kernel_size=1, bias=False),
            nn.BatchNorm2d(out_channels),
            nn.ReLU(inplace=True),
            nn.Conv2d(out_channels, out_channels, stride=stride, kernel_size=3, padding=1, bias=False),
            nn.BatchNorm2d(out_channels),
            nn.ReLU(inplace=True),
            nn.Conv2d(out_channels, out_channels * BottleNeck.expansion, kernel_size=1, bias=False),
            nn.BatchNorm2d(out_channels * BottleNeck.expansion),
        )

        self.shortcut = nn.Sequential()

        if stride != 1 or in_channels != out_channels * BottleNeck.expansion:
            self.shortcut = nn.Sequential(
                nn.Conv2d(in_channels, out_channels * BottleNeck.expansion, stride=stride, kernel_size=1, bias=False),
                nn.BatchNorm2d(out_channels * BottleNeck.expansion)
            )

    def forward(self, x):
        return nn.ReLU(inplace=True)(self.residual_function(x) + self.shortcut(x))

class ResNet(nn.Module):

    def __init__(self, block, num_block, num_classes=100):
        super().__init__()

        self.in_channels = 64

        self.conv1 = nn.Sequential(
            nn.Conv2d(3, 64, kernel_size=3, padding=1, bias=False),
            nn.BatchNorm2d(64),
            nn.ReLU(inplace=True))
        #we use a different inputsize than the original paper
        #so conv2_x's stride is 1
        self.conv2_x = self._make_layer(block, 64, num_block[0], 1)
        self.conv3_x = self._make_layer(block, 128, num_block[1], 2)
        self.conv4_x = self._make_layer(block, 256, num_block[2], 2)
        self.conv5_x = self._make_layer(block, 512, num_block[3], 2)
        self.avg_pool = nn.AdaptiveAvgPool2d((1, 1))
        self.fc = nn.Linear(512 * block.expansion, num_classes)

    def _make_layer(self, block, out_channels, num_blocks, stride):
        """make resnet layers(by layer i didnt mean this 'layer' was the
        same as a neuron netowork layer, ex. conv layer), one layer may
        contain more than one residual block

        Args:
            block: block type, basic block or bottle neck block
            out_channels: output depth channel number of this layer
            num_blocks: how many blocks per layer
            stride: the stride of the first block of this layer

        Return:
            return a resnet layer
        """

        # we have num_block blocks per layer, the first block
        # could be 1 or 2, other blocks would always be 1
        strides = [stride] + [1] * (num_blocks - 1)
        layers = []
        for stride in strides:
            layers.append(block(self.in_channels, out_channels, stride))
            self.in_channels = out_channels * block.expansion

        return nn.Sequential(*layers)

    def forward(self, x):
        output = self.conv1(x)
        output = self.conv2_x(output)
        output = self.conv3_x(output)
        output = self.conv4_x(output)
        output = self.conv5_x(output)
        output = self.avg_pool(output)
        output = output.view(output.size(0), -1)
        output = self.fc(output)

        return output

def resnet18():
    """ return a ResNet 18 object
    """
    return ResNet(BasicBlock, [2, 2, 2, 2])

def resnet34():
    """ return a ResNet 34 object
    """
    return ResNet(BasicBlock, [3, 4, 6, 3])

def resnet50():
    """ return a ResNet 50 object
    """
    return ResNet(BottleNeck, [3, 4, 6, 3])

def resnet101():
    """ return a ResNet 101 object
    """
    return ResNet(BottleNeck, [3, 4, 23, 3])

def resnet152():
    """ return a ResNet 152 object
    """
    return ResNet(BottleNeck, [3, 8, 36, 3])

Q4. 학습 가중치 초기화 (Xavier_normal 방법, kaiming_normal 방법)

📌 왜 초기화가 중요할까?

• 신경망 학습 초기에 가중치 분포가 너무 크거나 작으면
  ➜ 기울기 소실(vanishing) 또는 기울기 폭발(exploding) 발생
• 적절한 초기화는 입력/출력 variance를 일정하게 유지 → 안정적인 학습
  
  

PyTorch에서는 이런 초기화 전략을 쉽게 쓸 수 있게 torch.nn.init 모듈을 제공합니다. 모든 함수는 torch.no_grad() 모드에서 실행돼서 autograd에 기록되지 않아요.

🔹 주요 초기화 함수 요약

| 함수 | 역할 | 수식 / 특징 | | ——————————————– | ———————————– | ———————————————————— | | nn.init.constant_ | 텐서를 특정 상수 값으로 채움 | tensor[:] = val | | nn.init.ones_, nn.init.zeros_ | 1 또는 0으로 채움 | bias를 0으로 초기화할 때 자주 사용 | | nn.init.uniform_(a, b) | 균등분포 U(a, b)에서 샘플링 | 예: U(-0.1, 0.1) | | nn.init.normal_(mean, std) | 정규분포 N(mean, std²)에서 샘플링 | 예: N(0, 0.01) | | nn.init.trunc_normal_(mean, std, a, b) | 절단 정규분포 (값이 [a,b] 범위 안에만) | transformer 계열에서 자주 사용 | | nn.init.eye_ | 항등 행렬(I) 로 초기화 | Linear layer에 가끔 사용 | | nn.init.dirac_ | Conv 레이어에서 입력=출력 채널 연결 유지 | ID 매핑 효과 | | nn.init.sparse_ | 텐서를 희소 행렬(sparse) 로 초기화 | 각 column에 일부 값만 N(0, std²)로 채움 | | nn.init.orthogonal_ | 가중치를 직교행렬로 초기화 | 출력 간 상관관계 최소화 | | nn.init.xavier_uniform_ | Glorot uniform, 입출력 variance 균형 | U(-a, a) where a = gain * sqrt(6/(fan_in + fan_out)) | | nn.init.xavier_normal_ | Glorot normal | N(0, std²) where std = gain * sqrt(2/(fan_in + fan_out)) | | nn.init.kaiming_uniform_ | He uniform (ReLU용) | U(-bound, bound) with bound = gain * sqrt(3/fan_in) | | nn.init.kaiming_normal_ | He normal (ReLU용) | N(0, std²) where std = gain / sqrt(fan_in) | | nn.init.calculate_gain() | 활성함수별 gain (스케일링 상수) 계산 | 예: ReLU=√2, Tanh=5/3, LeakyReLU=√(2/(1+α²)) |

⚙️ calculate_gain() 자세히 보기

활성 함수별로 입력 분산을 유지하려면 gain(보정 계수)이 달라집니다.

비선형 함수	gain 값	비고
'linear' / 'conv2d'	1	기본
'sigmoid'	1
'tanh'	5/3 ≈ 1.6667
'relu'	√2 ≈ 1.414	He 초기화의 핵심
'leaky_relu'	√(2/(1+α²))	α=0.01이면 ≈1.414
'selu'	3/4	하지만 self-normalizing에서는 linear 권장

gain = nn.init.calculate_gain('relu')
w = torch.empty(64, 3, 3, 3)
nn.init.xavier_uniform_(w, gain=gain)

Xavier_normal 방법

• 논문: Glorot & Bengio (2010)
• 목표: 입출력 variance 동일하게 유지
• 적용: Sigmoid, Tanh 계열. ReLU에는 Kaiming이 더 적합.
• 공식:

nn.init.xavier_uniform_(layer.weight, gain=nn.init.calculate_gain('relu'))

⚡ Kaiming (He) 초기화

• 논문: He et al., 2015
• 목표: ReLU 함수에서 입력 분산 보존
• 공식:

• 두 버전 있음:
  • kaiming_uniform_: U(-bound, bound)
  • kaiming_normal_: N(0, std²)

nn.init.kaiming_normal_(conv.weight, mode='fan_out', nonlinearity='relu')

1) mode가 뭐냐?

Kaiming(He) 초기화에서 분산을 어디에서 보존할지를 고르는 옵션이야.

• mode=’fan_in’ → 순전파(forward) 에서 분산 보존 (가장 흔함, 기본값)
• mode=’fan_out’ → 역전파(backward) 에서 분산 보존

대부분 ReLU 계열 네트워크에선 fan_in 을 씀. 특정 이유(예: Deconv/특정 아키텍처의 안정성)를 위해 역전파 분산 보존이 필요하면 fan_out.

2) kaiming_uniform_의 bound와 kaiming_normal_의 std

Kaiming 초기화의 목표: ReLU/LeakyReLU 같은 비대칭 활성화에서도 신호 분산이 층을 지나며 유지되도록 가중치 분포를 설정.

👉 kaiming_uniform_의 bound 와 kaiming_normal_의 std 는 레이어의 fan 값과 활성함수에 맞춘 가중치 분포의 스케일일 뿐이고, BatchNorm/LayerNorm과는 무관해! (정규화 레이어 종류와 상관없이 “가중치 초기 분포”를 정하는 파라미터야.)

🧮 fan_in / fan_out 이란?

용어	의미
fan_in	입력 feature 수 (입력 채널 × 커널 크기)
fan_out	출력 feature 수 (출력 채널 × 커널 크기)

• 예: Conv2d(64, 128, kernel_size=3)
  → fan_in = 64×3×3, fan_out = 128×3×3

import torch.nn as nn

class MyNet(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv = nn.Conv2d(3, 64, 3, padding=1)
        self.fc = nn.Linear(64*32*32, 10)
        self.init_weights()

    def init_weights(self):
        nn.init.kaiming_normal_(self.conv.weight, mode='fan_out', nonlinearity='relu')
        nn.init.constant_(self.conv.bias, 0)
        nn.init.xavier_uniform_(self.fc.weight, gain=nn.init.calculate_gain('relu'))
        nn.init.zeros_(self.fc.bias)

정리

카테고리	대표 함수	주 용도
상수 초기화	constant_, zeros_, ones_	bias 또는 실험용
확률적 초기화	uniform_, normal_, trunc_normal_	임의 분포로 초기화
선형 보존형	eye_, dirac_	항등 또는 ID 매핑 보존
정규화 계열	xavier_*, kaiming_*	대부분의 CNN / MLP 기본
특수 목적	orthogonal_, sparse_	직교성, 희소성 부여