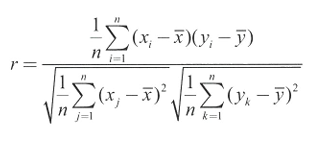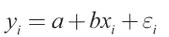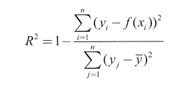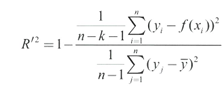7장.상관과 회귀

7.1 양적 변수 사이의 관계를 밝히다

2개의 양적 변수로 이루어진 데이터

• 상관과 회귀: 양적 변수 사이의 관계를 분석하는 또 다른 방법

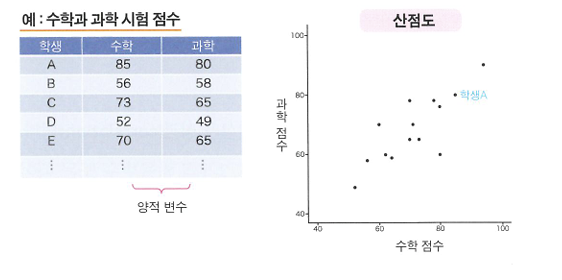
산점도

상관

• 상관
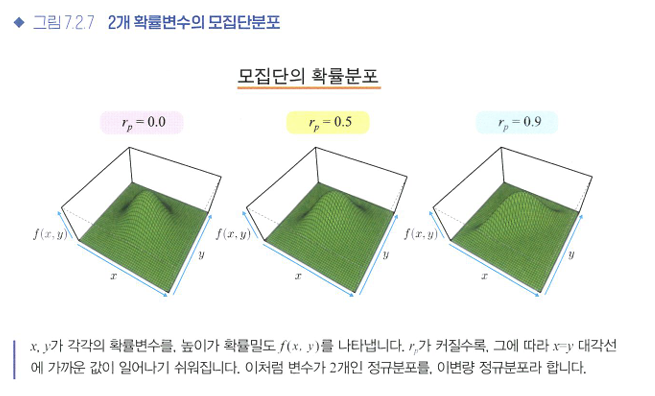
  • 2개 변수 사이의 관계성
  • 2개의 확률변수 또는 데이터 사이의 관계성 ❗상관이 있다고 해서 원인과 결과를 뜻하는 인과관계가 있는지까지는 알 수 없다

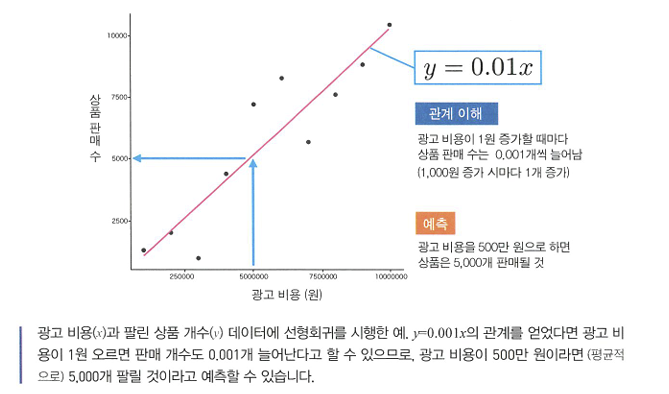
회귀

• 회귀: y=f(x)라는 함수를 통해 변수 사이의 관계를 공식화하는 것
  • x: 설명변수/독립변수
  • y: 반응변수/종속변수

7.2 상관관계

피어슨 상관계수

• 피어슨 상관계수: 2개 양적 변수 사이의 선형관계가 얼마나 직선 관계에 가까운가를 평가
  • -1 <= r <= 1
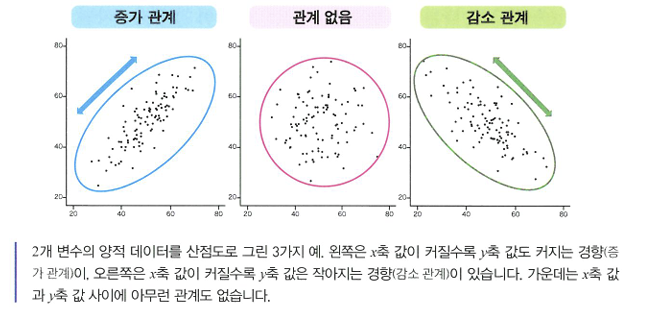
  • 양의 상관: 함께 커짐
  • 음의 상관: 함께 작아짐

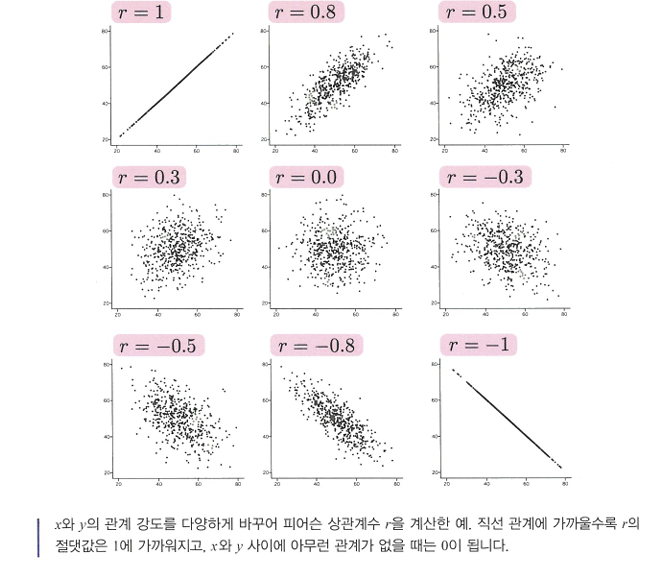
  • r	: 1에 가까울 수록 관계는 직선에 가까워짐

-> 분자: 공분산 / 분모: x와 y 각각의 표준편차

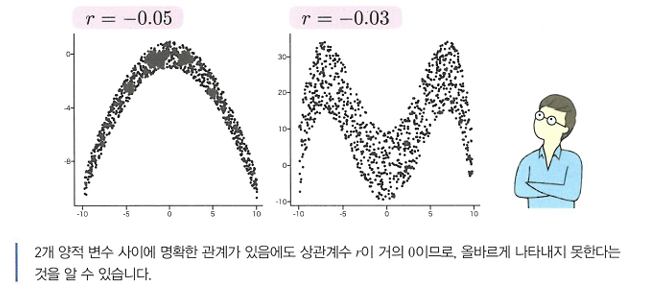
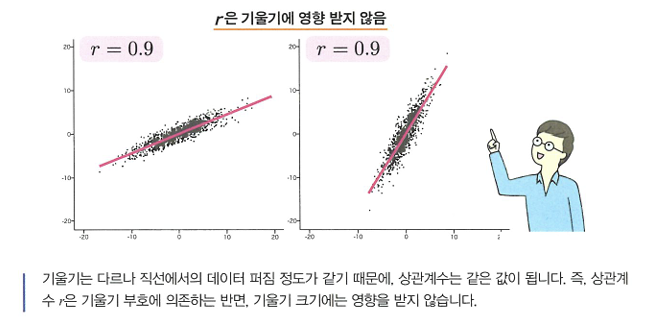
🔖상관계수 r은 선형관계를 나타낸다.

• 주의할 점
  1. 피어슨 상관계수 r은 2개 양적 변수의 ‘선형’ 관계성 강도를 정량화 한 것 -> 비선형 관계는 정량화X

  

  1. 직선의 기울기 크기는 관계가 없다.

  

🔖상관계수가 같은 다양한 데이터

❗데이터로 상관계수를 계산하기만 하고서 산점도 짐작하는 것은 위험하다!

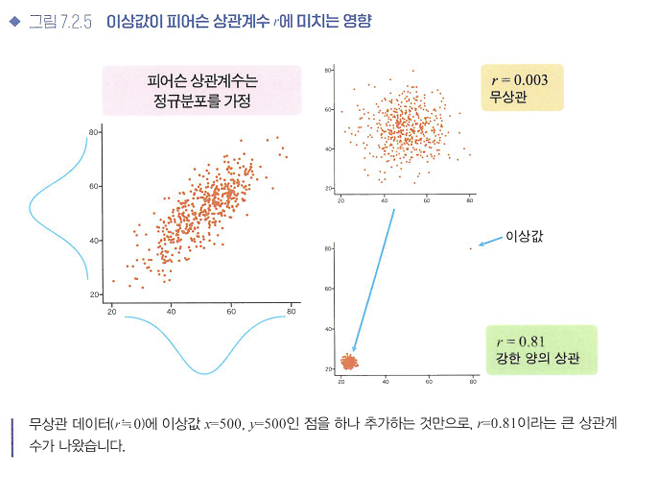
🔖정규성 검사

• 피어슨 상관계수는 모수적인 방법

❗계산전 샤피로-월크 검정 등으로 정규성 검정!

비모수 상관계수

• 스피어만 순위상관계수: 적어도 하나 이상에 정규성이 없을 때는, 비모수 상관계수의 사용 권장
  • 데이터 값을 각 축에서 크기 순으로 나열했을 때의 순위로 변환한 다음 식 적용
• 켄달 순위상관계수: 표본크기 n이 매우 작을 때

🔖상관계수 사용 시 주의할 점

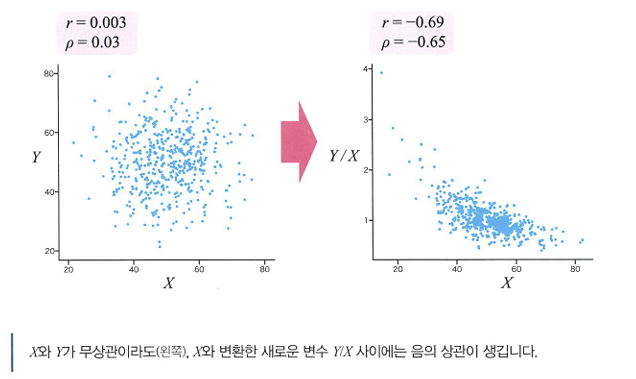
• 2개 변수가 처음부터 종속 관계일 때는 주의가 필요

상관계수의 가설검정

🔖상관계수의 가설검정

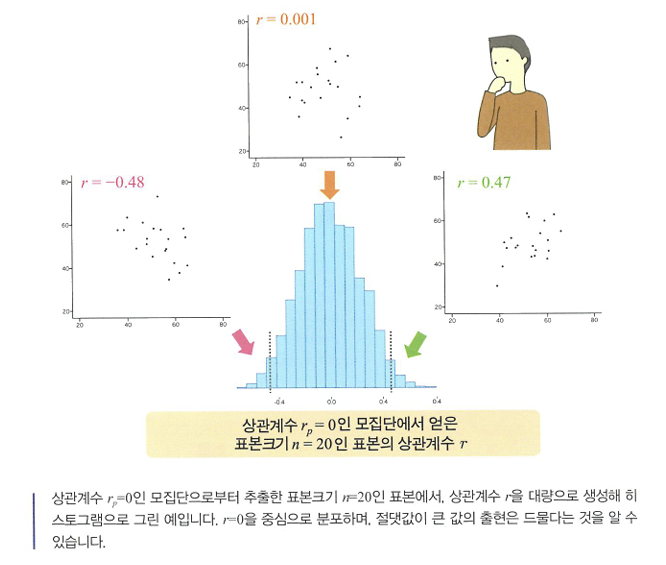
• 상관계수 r은 모집단분포에서 무직위추출로 얻은 표본에서 계산한 값으로, rp의 추정값이 된다.

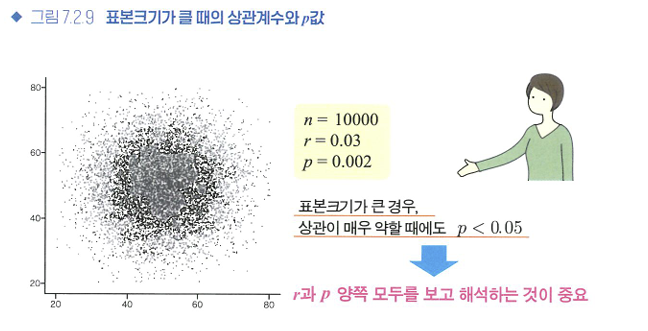
🔖표본크기와 가설검정

비선형상관

• 일반적인 원리: X가 Y에 관해, 또는 Y가 X에 관해 어느 정도의 정보를 포함하는지의 관점에서 관계성 강도를 정량화하는 것.

7.3 선형회귀

회귀분석이란?

• 단순회귀: 설명변수가 하나
• 다중회귀: 설명변수가 여러개
• 회귀계수: f(x)의 형태를 결정하는 파라미터 a, b
• 회귀모형

💡회귀분석시 중요한 점

➕선형회귀

• 회귀분석에서 사용하는 회귀식이 ‘파라미터에 관한’ 1차식이 될 때

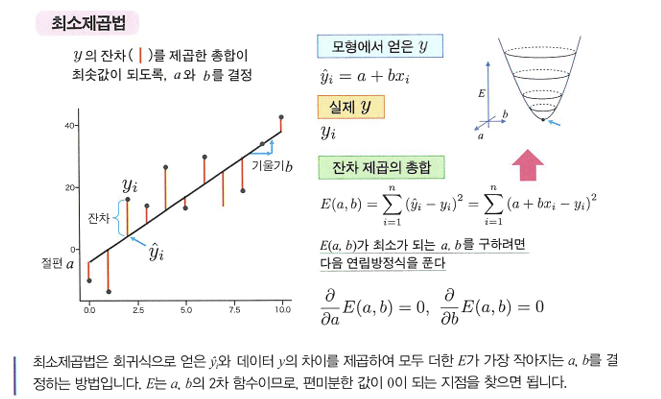
🔖최소제곱법

• 최소제곡법: 데이터와 모형 차이의 제곱을 모두 더한 값 E를 최소화하는 방법

회귀계수

• 오차는 x와는 관계가 없고 평균 0, 분산 시그마^2인 어떤 확률분포를 따르는 확률변수이다.
• 최소제곱법으로 얻은 선형회귀 파라미터는 모집단 파라미터의 비편향추정량이 된다.

• 최량선형비편향추정량: 최소제곱법으로 얻은 추정량은 비편향추정량 중에서도 가장 정밀도가 높은 비편향추정량이 된다.

🔖회귀계수의 가설검정

• 회귀계수를 대상으로 가설검정을 시행할 수 있다.

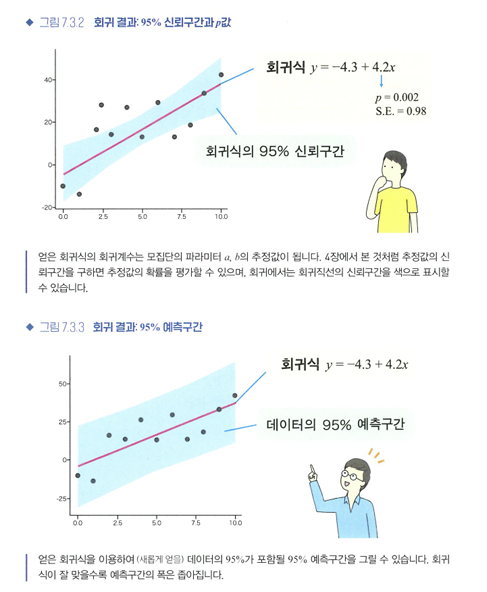
🔖95% 신뢰구간

• 모집단의 회귀계수를 추정하면 신뢰구간을 얻을 수 있다.

🔖95% 예측구간

• 추정한 회귀모형을 기반으로 데이터 그 자체가 분포하는 구간을 그릴 수 있는데, 이를 예측구간이라 한다.

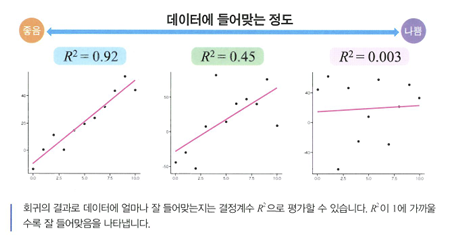
결정계수

• 결정계수: 회귀식이 잘 들어맞는지 평가하는 지표

• 조정 결정계수: 설명변수가 많을 때 이용

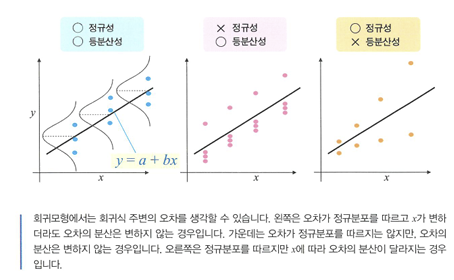
오차의 등분산성과 정규성

• 등분산성을 확인하려면 브루쉬-페이건 검정을 이용

설명변수와 반응변수

1. 한쪽 변수로 다른 한쪽 변수를 설명하고자 할 때
2. 인과효과를 알고싶을 때
3. 데이터를 예측하고 싶을 때