Post

8.수치 시뮬레이션으로 소비자의 행동을 예측하는 테크닉 10

Posted Updated
By Lee Jae Hui
9 min read
8.수치 시뮬레이션으로 소비자의 행동을 예측하는 테크닉 10

🔖전제조건

  • links.csv:
    • 재구매 고객 20명의 SNS 연결 상태
    • 연결이 있으면 1, 없으면 0
  • links_members.csv:
    • 모든 재구매 고객 540명의 SNS 연결 상태
  • info_members.csv:
    • 모든 재구매 고객 540명의 2년간 매월 이용 현황이 저장
    • 이용 실적이 있으면 1, 없으면 0

071.인간관계 네트워크를 가시화해 보자

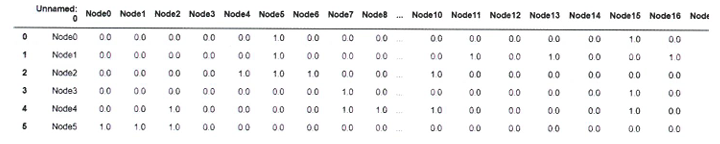
데이터 불러오기

1
2
3
4

import pandas as pd

df_links = pd.read_csv("links.csv")
df_links

alt text

네트워크 가시화

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

import networkx as nx
import matplotlib.pyplot as plt

# 그래프 객체 생성
G = nx.Graph()
# 네트워크 속성 부여

# 노드 설정
NUM = len(df_links.index)
# 노드의 갯수
for i in range(1,NUM+1):
    node_no = df_links.columns[i].strip("Node")
    # strip: 전달한 인자가 제거된 문자열의 복사본을 돌려줍니다.
    G.add_node(str(node_no))

# 엣지 설정
for i in range(NUM):
    for j in range(NUM):
        node_name = "Node" + str(j)
        if df_links[node_name].iloc[i]==1:
            G.add_edge(str(i),str(j))
        
# 그리기
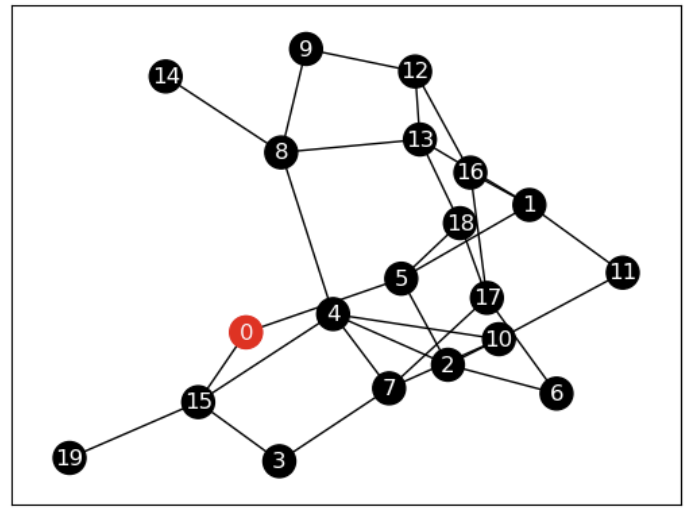
nx.draw_networkx(G,node_color="k", edge_color="k", font_color="w")
# 연결이 많은 노드를 중ㅅㅁ에 오게 자동으로 위치 결정
plt.show()

072.입소문에 의한 정보 전파 모습을 가시화해 보자

입소문 전파 계산

❗10개의 연결 중 하나의 확률(10%의 확률)로 소문이 전파된다라고 가정

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

import numpy as np

# 입소문의 전파 여부를 확률적으로 결정.
def determine_link(percent):
    rand_val = np.random.rand()
    # np.random.rand(): 0~1의 균일분포 표준정규분포 난수를 생성.
    if rand_val<=percent:
        return 1
    else:
        return 0

# 입소문을 시뮬레이션
def simulate_percolation(num, list_active, percent_percolation):
    # num: 사람 수 / list_active: 각각의 노드에 입소문이 전달됐는지를 1 or 0 / percent_percolation: 입소문을 일으킬 확률
    for i in range(num):
        if list_active[i]==1:
            for j in range(num):
                node_name = "Node" + str(j)
                if df_links[node_name].iloc[i]==1:
                    if determine_link(percent_percolation)==1:
                        list_active[j] = 1
    return list_active

percent_percolation = 0.1
# 입소문을 일으킬 확률 10%
T_NUM = 36
# 36개월 반복
NUM = len(df_links.index)
# 사람 수
list_active = np.zeros(NUM)
list_active[0] = 1
# 첫번째 사람에게 입소문 냄.

list_timeSeries = []
for t in range(T_NUM):
    list_active = simulate_percolation(NUM, list_active, percent_percolation)
    list_timeSeries.append(list_active.copy())

입소문 전파 가시화

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# 액티브 노드 가시화 #
def active_node_coloring(list_active):
    #print(list_timeSeries[t])
    list_color = []
    for i in range(len(list_timeSeries[t])):
        if list_timeSeries[t][i]==1:
            list_color.append("r")
        else:
            list_color.append("k")
    #print(len(list_color))
    return list_color

# 그리기
t = 0
nx.draw_networkx(G,font_color="w",node_color=active_node_coloring(list_timeSeries[t]))
plt.show()

alt text

1
2
3
4

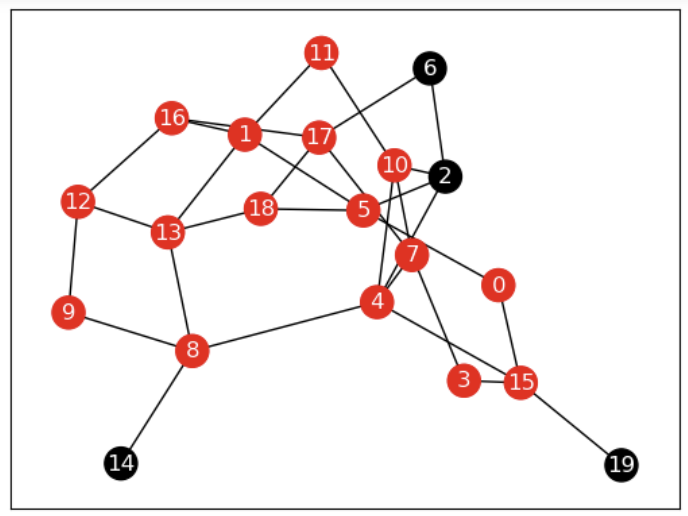
# 그리기
t = 11
nx.draw_networkx(G,font_color="w",node_color=active_node_coloring(list_timeSeries[t]))
plt.show()

alt text

1
2
3
4

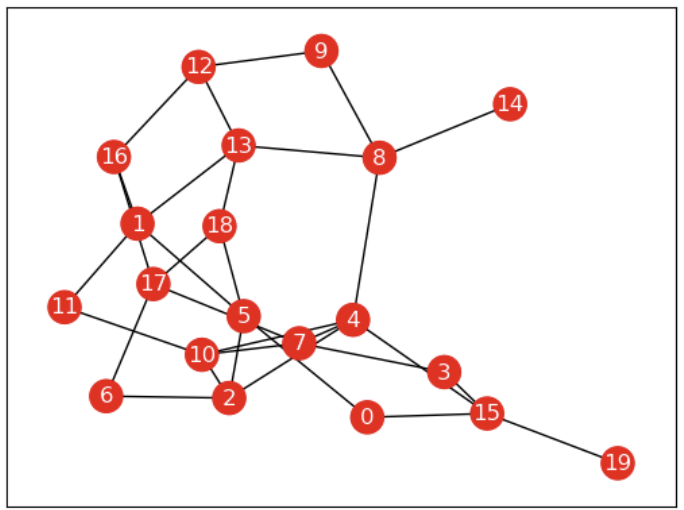
# 그리기
t = 35
nx.draw_networkx(G,font_color="w",node_color=active_node_coloring(list_timeSeries[t]))
plt.show()

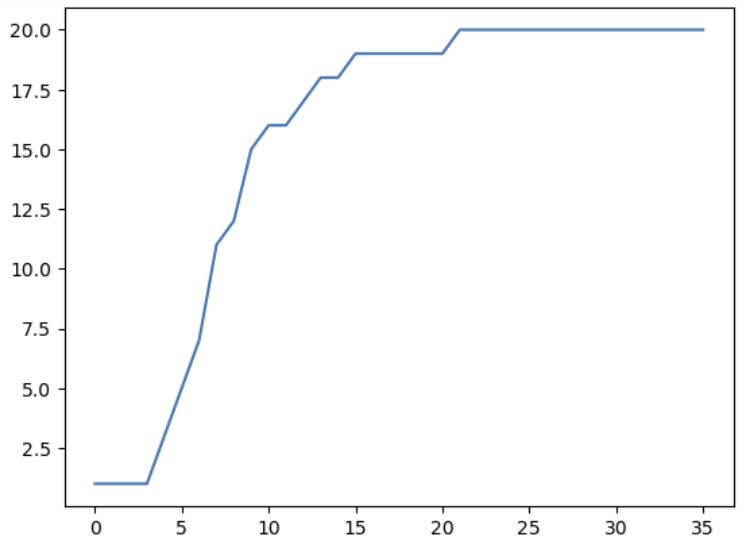
alt text

073.입소문 수의 시계열 변화를 그래프화해 보자

입소문 수의 시계열 변화

1
2
3
4
5
6
7

# 시계열 그래프 그리기
list_timeSeries_num = []
for i in range(len(list_timeSeries)):
    list_timeSeries_num.append(sum(list_timeSeries[i]))

plt.plot(list_timeSeries_num)
plt.show()

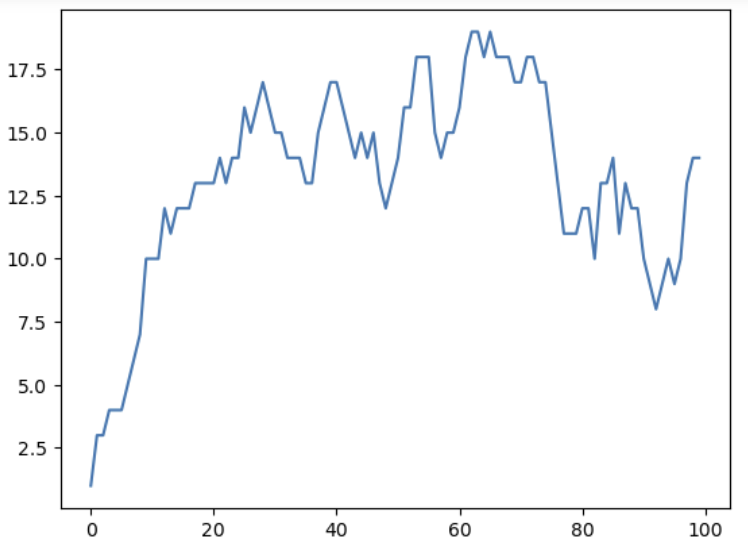
alt text

074. 회원 수의 시계열 변화를 시뮬레이션해 보자

입소문을 통해 스포츠 센터의 이용 상황이 어떻게 변화해가는지 시뮬레이션

회원수의 시계열변화를 시뮬레이션해보자

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

def simulate_population(num, list_active, percent_percolation, percent_disapparence,df_links):
    # 확산 #
    for i in range(num):
        if list_active[i]==1:
            for j in range(num):
                if df_links.iloc[i][j]==1:
                    if determine_link(percent_percolation)==1:
                        list_active[j] = 1
    # 소멸 #
    for i in range(num):
        if determine_link(percent_disapparence)==1:
            list_active[i] = 0
    return list_active

percent_percolation = 0.1
percent_disapparence = 0.05
T_NUM = 100
NUM = len(df_links.index)
list_active = np.zeros(NUM)
list_active[0] = 1

list_timeSeries = []
for t in range(T_NUM):
    list_active = simulate_population(NUM, list_active, percent_percolation, percent_disapparence,df_links)
    list_timeSeries.append(list_active.copy())

# 시계열 그래프 그리기
list_timeSeries_num = []
for i in range(len(list_timeSeries)):
    list_timeSeries_num.append(sum(list_timeSeries[i]))

plt.plot(list_timeSeries_num)
plt.show()

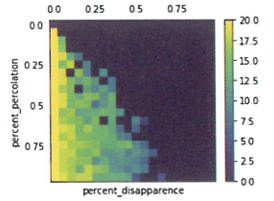
alt text

075.파라미터 전체를 ‘상관관계’를 보면서 파악해 보자

파라미터 전체 모습

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

# 상관관계 계산
print("상관관계 계산시작")
T_NUM = 100
NUM_PhaseDiagram = 20
phaseDiagram = np.zeros((NUM_PhaseDiagram,NUM_PhaseDiagram))
for i_p in range(NUM_PhaseDiagram):
    for i_d in range(NUM_PhaseDiagram):
        percent_percolation = 0.05*i_p
        percent_disapparence = 0.05*i_d
        list_active = np.zeros(NUM)
        list_active[0] = 1
        for t in range(T_NUM):
            list_active = simulate_population(NUM, list_active, percent_percolation, percent_disapparence,df_links)
        phaseDiagram[i_p][i_d] = sum(list_active)
print(phaseDiagram)

# 표시
plt.matshow(phaseDiagram)
plt.colorbar(shrink=0.8)
plt.xlabel('percent_disapparence')
plt.ylabel('percent_percolation')
plt.xticks(np.arange(0.0, 20.0,5), np.arange(0.0, 1.0, 0.25))
plt.yticks(np.arange(0.0, 20.0,5), np.arange(0.0, 1.0, 0.25))
plt.tick_params(bottom=False,
                left=False,
                right=False,
                top=False)
plt.show()

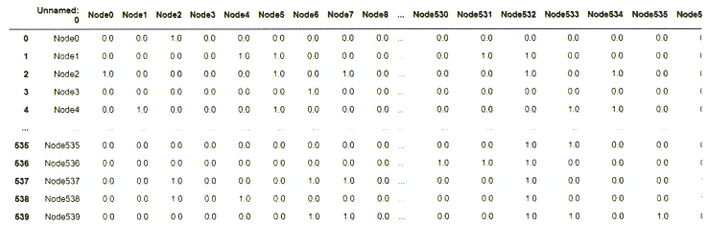
alt text

076.실제 데이터를 불러와보자

  • links_members.csv: 540명 각각의 SNS 연결을 저장
  • info_members.csv:
    • 540명의 24개월간 이용 현황
    • 1: 이용한 달
    • 0: 이용하지 않은 달
1
2
3
4
5

import pandas as pd

df_mem_links = pd.read_csv("links_members.csv")
df_mem_info = pd.read_csv("info_members.csv")
df_mem_links

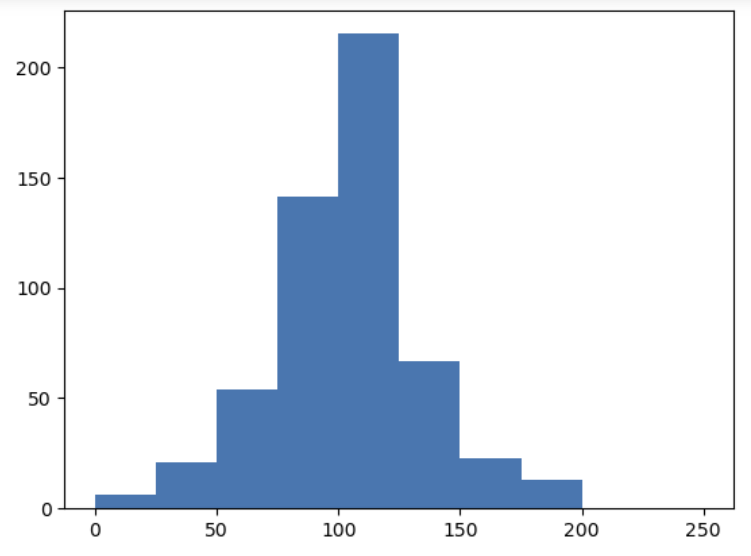
alt text

077.링크 수의 분포를 가시화해 보자

  • 네트워크 구조
    • 스몰 월드형: 몇 안 되는 스텝으로 전원이 연결됨
    • 스케일 프리형: 소수의 연결

링크 수의 분포

1
2
3
4
5
6
7

NUM = len(df_mem_links.index)
array_linkNum = np.zeros(NUM)
for i in range(NUM):
    array_linkNum[i] = sum(df_mem_links["Node"+str(i)])

plt.hist(array_linkNum, bins=10,range=(0,250))
plt.show()

alt text

  • 스케일 프리형 이라면? -> 링크를 많이 가진 허브가 작동하지 않으면 입소문이 중간에 퍼지지 않음.
  • 이 분포는 허브에 의존하지 않고 입소문이 퍼지기 쉽다.

078.시뮬레이션을 위해 실제 데이터로부터 파라미터를 추정하자

⭐중요한 파라미터: percent_percolation, percent_disapparence

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

NUM = len(df_mem_info.index)
# 사람수
T_NUM = len(df_mem_info.columns)-1
# 개월수
# 소멸 확률 추정 #
count_active = 0
count_active_to_inactive = 0
for t in range(1,T_NUM):
    for i in range(NUM):
        if (df_mem_info.iloc[i][t]==1):
            count_active_to_inactive += 1
            if (df_mem_info.iloc[i][t+1]==0):
                count_active += 1
estimated_percent_disapparence = count_active/count_active_to_inactive
# 1스텝 전과 비교해서 활성이 비활성으로 변화한 비율!

# 확산 확률 추정 #
count_link = 0
count_link_to_active = 0
count_link_temp = 0
for t in range(T_NUM-1):
    df_link_t = df_mem_info[df_mem_info[str(t)]==1]
    # 활동중인 애들만 뽑아
    temp_flag_count = np.zeros(NUM)
    for i in range(len(df_link_t.index)):
        # 활동중인 애들중...
        df_link_temp = df_mem_links[df_mem_links["Node"+str(df_link_t.index[i])]==1]
        # "Node"+str(df_link_t.index[i])와 link가 되어있는 애들만 뽑아!
        for j in range(len(df_link_temp.index)):
            if (df_mem_info.iloc[df_link_temp.index[j]][t]==0):
                # t달에 비활동 
                if (temp_flag_count[df_link_temp.index[j]]==0):
                    count_link += 1
                if (df_mem_info.iloc[df_link_temp.index[j]][t+1]==1):
                    # t+1달에 활동이면
                    if (temp_flag_count[df_link_temp.index[j]]==0):
                        temp_flag_count[df_link_temp.index[j]] = 1 
                        count_link_to_active += 1
estimated_percent_percolation = count_link_to_active/count_link

print(estimated_percent_disapparence)
# 0.10147163541419416

print(estimated_percent_percolation)
# 0.025184661323275185

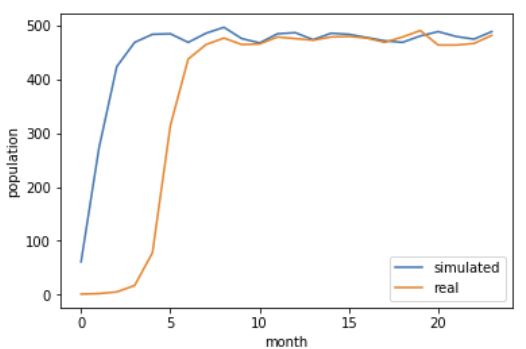
079.실제 데이터와 시뮬레이션을 비교하자

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

percent_percolation = 0.025184661323275185
percent_disapparence = 0.10147163541419416
T_NUM = 24
NUM = len(df_mem_links.index)
# 사람 수
list_active = np.zeros(NUM)
list_active[0] = 1
list_timeSeries = []
for t in range(T_NUM):
    list_active = simulate_population(NUM, list_active, percent_percolation, percent_disapparence,df_mem_links)
    list_timeSeries.append(list_active.copy())

list_timeSeries_num = []
for i in range(len(list_timeSeries)):
    list_timeSeries_num.append(sum(list_timeSeries[i]))
# 개월별 1과 0의 합

T_NUM = len(df_mem_info.columns)-1
# 처음에 이상한 열 빼고 개월수
list_timeSeries_num_real = []
for t in range(0,T_NUM):
    list_timeSeries_num_real.append(len(df_mem_info[df_mem_info[str(t)]==1].index))
    # 해당 달의 실제 활동 중이던 사람의 수

plt.plot(list_timeSeries_num, label = 'simulated')
plt.plot(list_timeSeries_num_real, label = 'real')
plt.xlabel('month')
plt.ylabel('population')
plt.legend(loc='lower right')
plt.show()

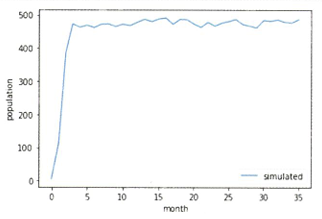
alt text

080.시뮬레이션으로 미래를 예측해 보자

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

percent_percolation = 0.025184661323275185
percent_disapparence = 0.10147163541419416
T_NUM = 36
NUM = len(df_mem_links.index)
list_active = np.zeros(NUM)
list_active[0] = 1
list_timeSeries = []
for t in range(T_NUM):
    list_active = simulate_population(NUM, list_active, percent_percolation, percent_disapparence,df_mem_links)
    list_timeSeries.append(list_active.copy())

list_timeSeries_num = []
for i in range(len(list_timeSeries)):
    list_timeSeries_num.append(sum(list_timeSeries[i]))

plt.plot(list_timeSeries_num, label = 'simulated')
plt.xlabel('month')
plt.ylabel('population')
plt.legend(loc='lower right')
plt.show()

alt text

데비&추천시스템, 파이썬 데이터분석 실무 테크닉 100
Khuda ML data
This post is licensed under CC BY 4.0 by the author.

Trending Tags

data Khuda ML