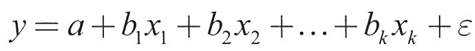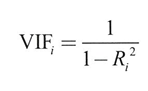8장 통계 모형화

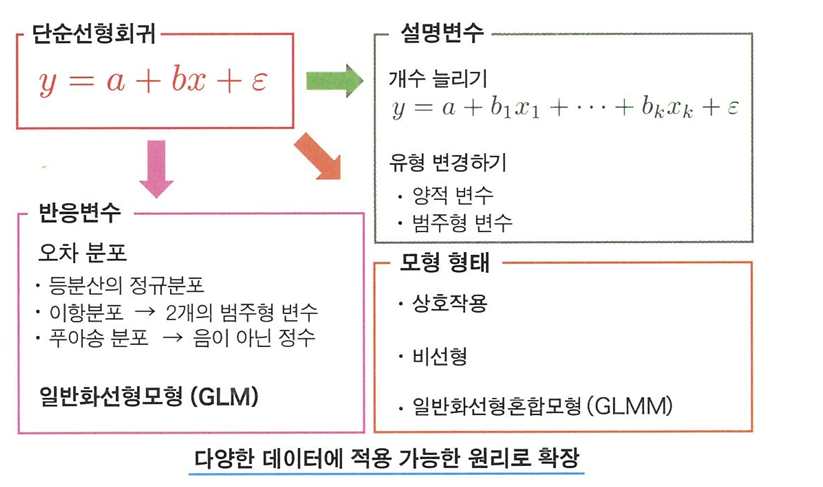
8.1 선형회귀 원리의 확장

선형회귀는 다양한 해석 방법의 기초

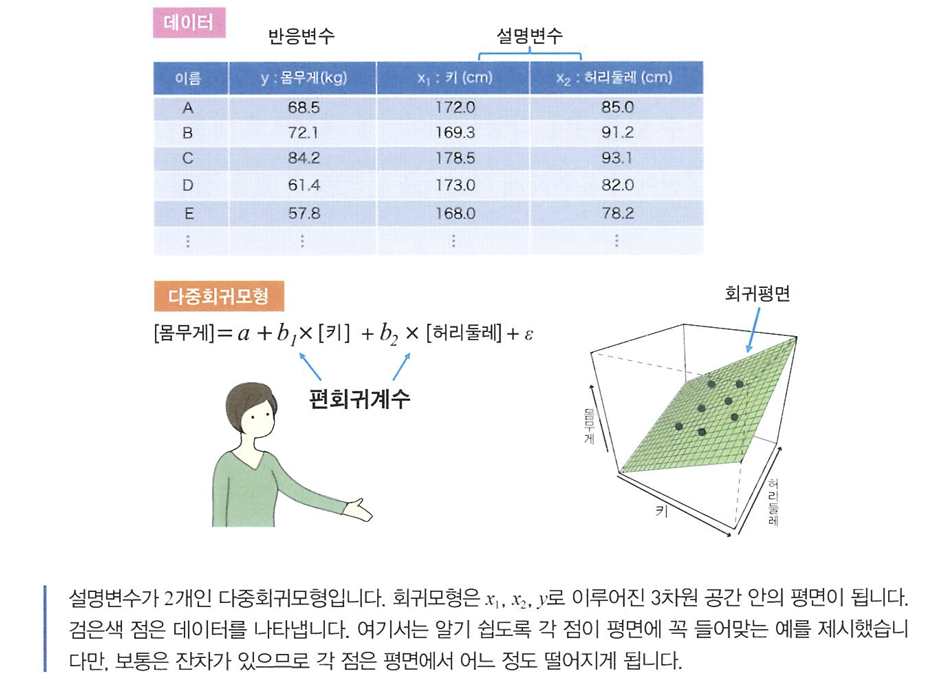
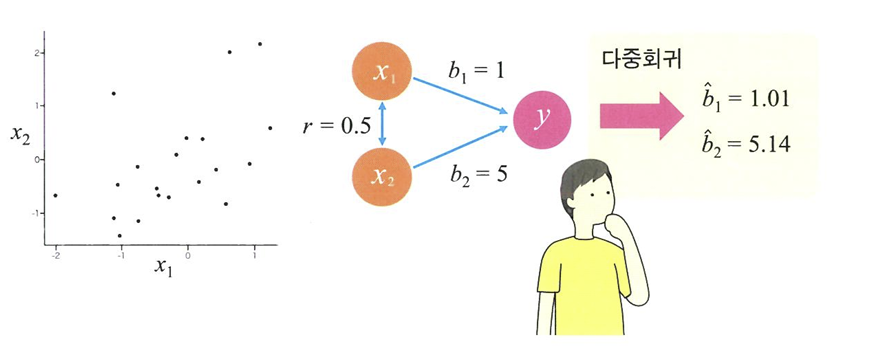
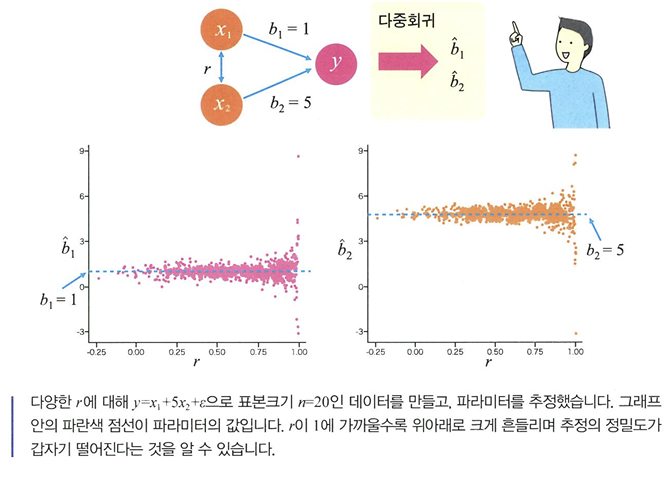
다중회귀

• 다중회귀: 설명변수가 여러 개

• 편회귀계수: b1, b2
• 회귀평면: 설명 변수가 2개일 때의 그래프

🔖다중회귀 결과를 읽는 방법

• 주목: 편회귀계수 / 유의성
• F통계량에서 얻은 P값: 편회귀계수가 모두 0인 모형(R^2=0)을 귀무가설로 하여, 회귀모형 설명력의 유의성을 조사

편회귀계수

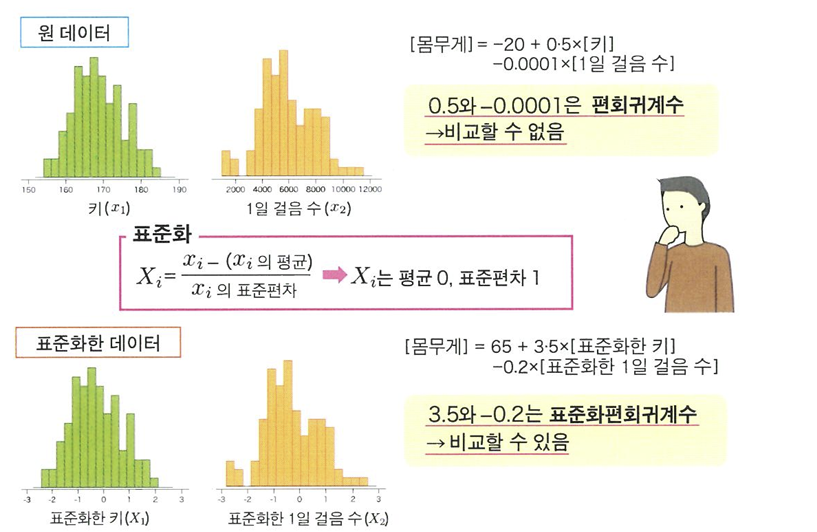
🔖표준화편회귀계수

❗회귀분석에서 구한 편회귀계수는 설명변수의 데이터 퍼짐 정도나 단위에 따라 크게 달라지기 때문에 편회귀계수끼리 비교할 수 없음

• 표준화편회귀계수: 편회귀계수 비교 위해 필요
  • 회귀분석을 진행하기 전에 각각의 설명변수를 평균 0, 표준편차 1로 변환한 다음, 회귀분석을 시행하여 구한 회귀계수
  • 각 설명변수가 표준편차 단위에서 1 늘었을 때 반응변수의 증감

🔖편회귀계수의 해석

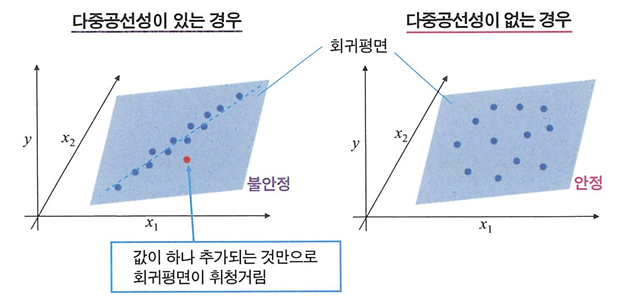
• 상관계수가 1에 가까운 강한 상관이 있을 경우 -> 다중 공선성 의심!

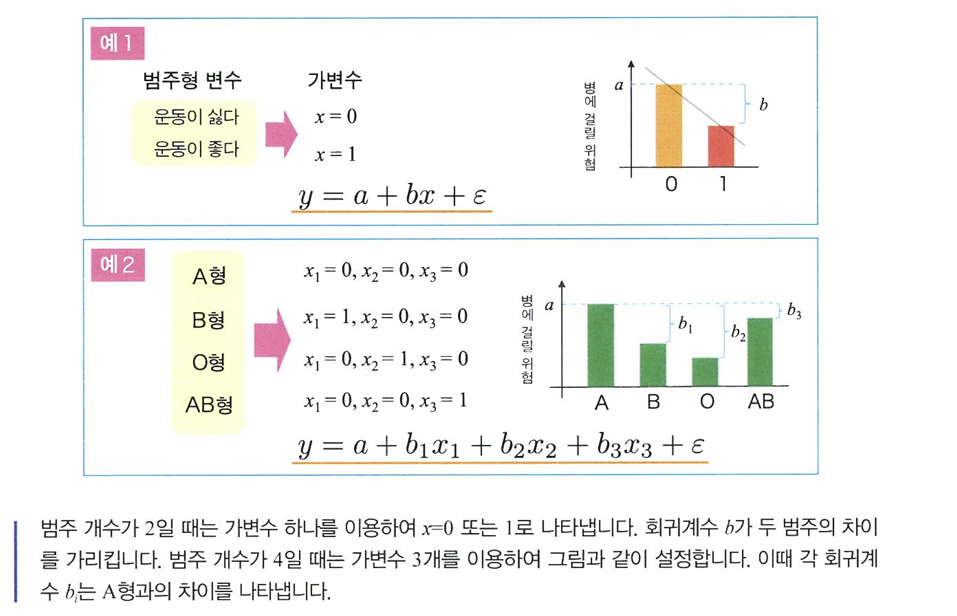
범주형 변수를 설명변수로

• 가변수 :0 or 1 -> 설명변수로 이용

🔖범주가 3개 이상일 때

1. 가변수를 (범주 개수 - 1)개 준비
2. 각 변수에 0또는 1 대입

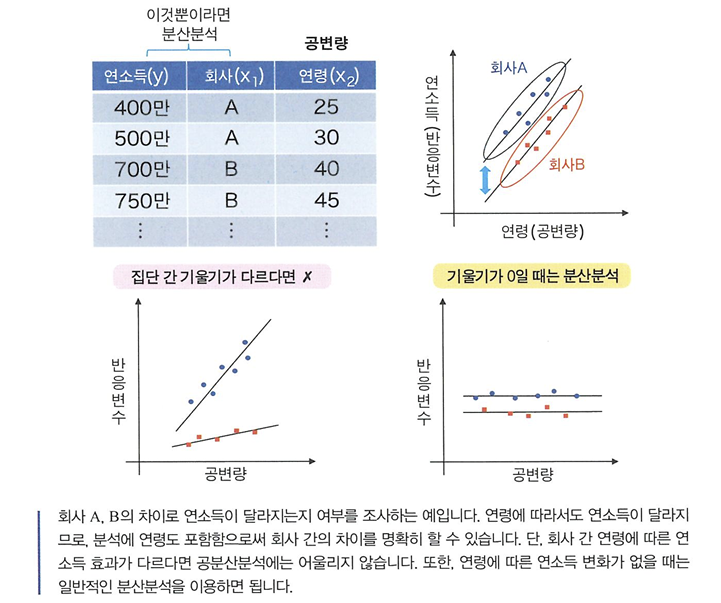
공분산분석

• 공분산분석: 일반적인 분산분석에 이용하는 데이터와 함께 양적 변수 데이터가 있는 경우에 후보가 되는 방안
  • 공변량: 새로 추가한 양적 변수

🔖공분산분석 이용 조건

1. 집단 간 회귀의 기울기가 서로 다르지 않을 것(상호작용이 X)
2. 회귀계수가 0이 아니어야 함(기울기의 유의성 검정에서 유의미하다면 만족)

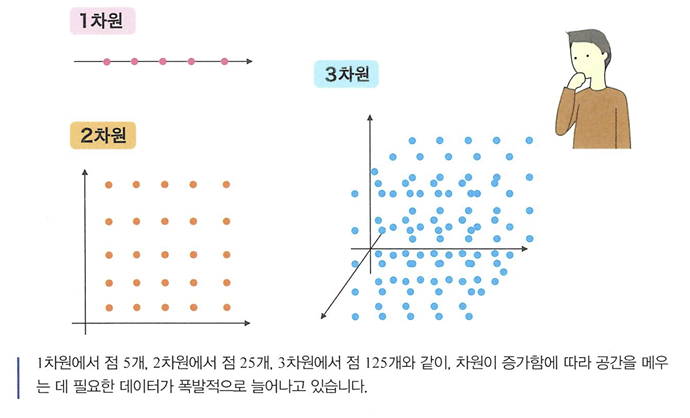
고차원 데이터 문제

• 차원의 저주: 차원이 늘어날수록 파라미터 추정에 필요한 데이터 양이 폭발적으로 증가한다.
• 차원이 증가할 수록 다중공선성 문제가 쉽게 일어남.

다중공선성

• 다중공선성: 설명변수가 여러 개인 다중회귀에서 설명변수 사이에 강한 상관이 있는 경우

🔖분산팽창인수 VIF

• 설명변수 xi의 VIFi는, Ri^2을 이용

• 해석
  • VIF>10: 2개 사이의 상관이 아주 강함
    => 서로 상관이 있는 2개 변수 중 하나 삭제 / 차원 축소 이용

8.2 회귀모형의 형태 바꾸기

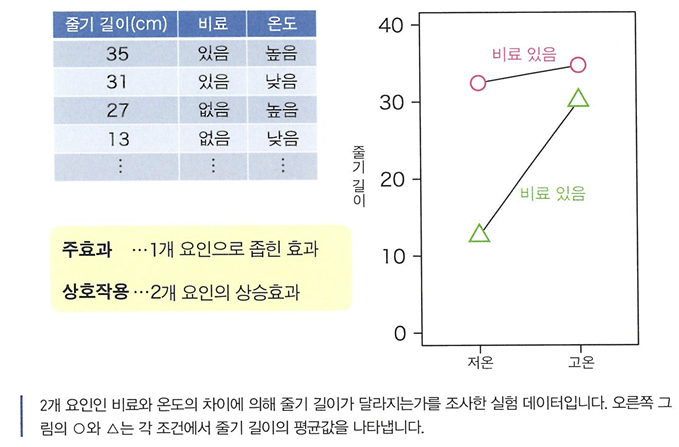
상호작용

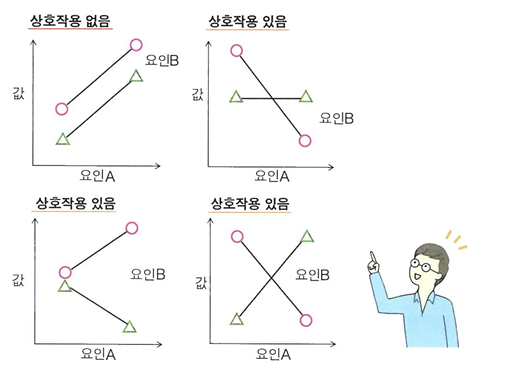
상호작용: 현실 데이터에서는 xi가 1 증가했을 때의 y 증가 방식이, 또 다른 설명변수의 영향을 받을 수 있는데 이러한 상승효과를 일컫는 말(cxixj로 도입 가능)

🔖주의

🔖넣는경우

이원배치 분산분석

• 일원배치 분산분석: 하나의 요인만 다룸
• 다원배치 분산분석: 여러 개의 요인을 동시에 고려
  • 이원배치 분산분석

• 상호작용항 c1 유의미 x -> 주효과 그대로 평가
• 상호작용항 c1 유의미 -> 주효과를 하위 검정으로 평가

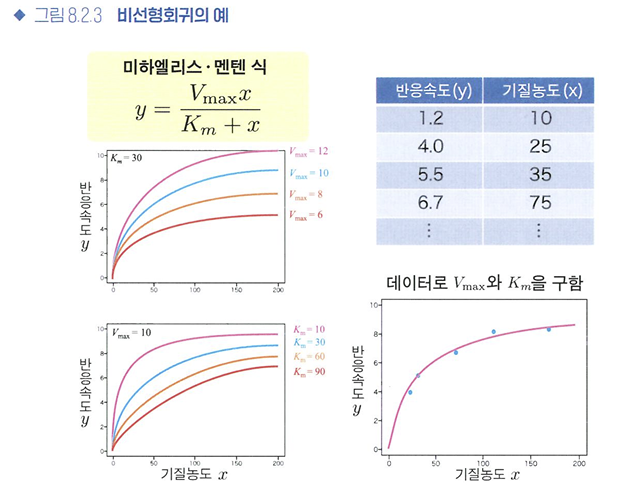
비선형회귀

• 예측 중요 -> 비선형 / 해석 중요 -> 고민

8.3 일반화선형모형의 개념

선형회귀 원리 확장하기

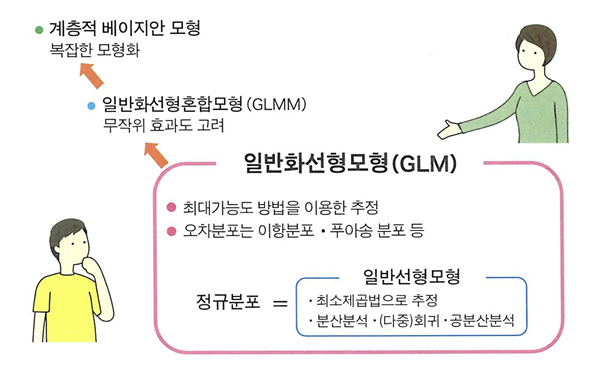
• 일반선형모형: 최소제곱법을 이용하여 파라미터 추정
• 일반화선형모형: 최소제곱법이 아닌 확률분포에 기반한 최대가능도 방법으로 회귀모형을 추정

• 통계 모형화: 데이터 성질을 고려하면서 확률 모형을 가정하고, 파라미터를 추정하여 모형을 평가하는 일련의 작업

🔖선형회귀가 적절하지 않은 상황