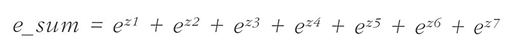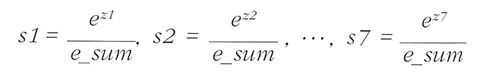4.다양한 분류 알고리즘

Posted Aug 13, 2024 Updated Aug 13, 2024

By Lee Jae Hui

21 min read

4.다양한 분류 알고리즘

4.1 로지스틱 회귀

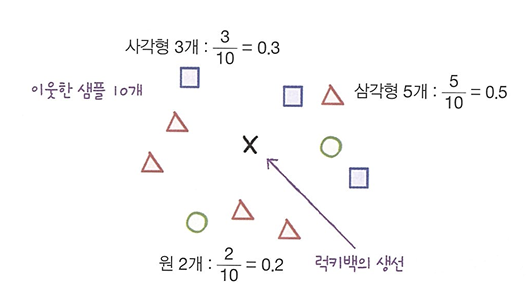
K-최근접 이웃 분류기로 클래스 확률 계산

생선 종류: 7종류
특성: 길이, 높이, 두께, 대각선 길이, 무게

데이터 준비하기

🔖 데이터 준비

  
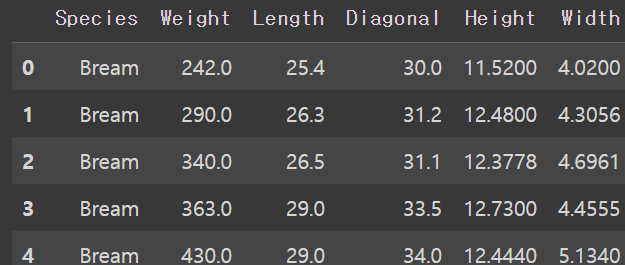
import pandas as pd
fish = pd.read_csv('https://bit.ly/fish.csv')
fish.head()

  
# 어떤 종류의 생선이 있는지 알아보자!
print(pd.unique(fish['Species']))
# ['Bream' 'Roach' 'Whitefish' 'Parkki' 'Perch' 'Pike' 'Smelt']

🔖 train과 target

target은 Species 열
입력 데이터는 나머지 5개의 열

  
fish_input = fish[['Weight','Length','Diagonal','Height','Width']].to_numpy()
print(fish_input[:5])

  
fish_target = fish['Species'].to_numpy()

🔖 훈력 세트와 테스트 세트

  
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(fish_input, fish_target, random_state = 42)

🔖 표준화 전처리

  
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)

K-최근접 이웃 분류기의 확률 예측

  
from sklearn.neighbors import KNeighborsClassifier
kn = KNeighborsClassifier(n_neighbors = 3)
kn.fit(train_scaled, train_target)
print(kn.score(train_scaled, train_target))
print(kn.score(test_scaled, test_target))
# 0.8907563025210085
# 0.85

다중 분류 by K-최근접 이웃 분류기

다중 분류: 타깃 데이터에 2개 이상의 클래스가 포함된 문제
predict_probe(): 클래스별 확률값 반환
round(): 소수점 첫째 자리에서 반올림
- decimals(매개변수): 유지할 소수점 아래 자릿수를 지정할 수 있다.

  
import numpy as np
# 타깃값의 순서는 문자일 경우 알파벳 순으로 매겨짐.
print(kn.classes)
# ['Bream' 'Parkki' 'Perch' 'Pike' 'Roach' 'Smelt' 'Whitefish']
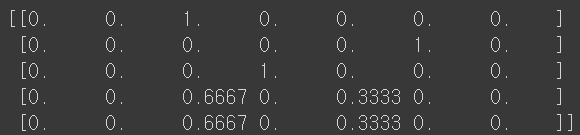
proba = kn.predict_proba(test_scaled[:5])
print(np.round(proba, decimals=4))
# 소수점 네 번째 자리까지 표기.

네 번째 샘플의 최근접 이웃의 클래스를 확인해보자.

  
distances, indexes = kn.kneighbors(test_scaled[3:4])
# kneighbors() 메서드의 입력은 2차원 배열이어야 합니다. 이를 위해 넘파이 배열의 슬라이싱 연산자를 사용했습니다. 슬라이싱 연산자는 하나의 샘플만 선택해도 항상 2차원 배열이 만들어집니다.
print(train_target[indexes])
# [['Roach' 'Perch' 'Perch']]

❗3개의 최근접 이웃을 사용하기에 확률은 0/3, 1/3, 2/3, 3/3이 전부이다!

로지스틱 회귀

로지스틱 회귀: 분류 모델.
- 선형 방정식을 학습한다.
  z = a x (Weight) + b x (Length) + c x (Diagonal) + d x (Height) + e x (Width) + f
- a, b, c, d, e는 가중치 or 계수
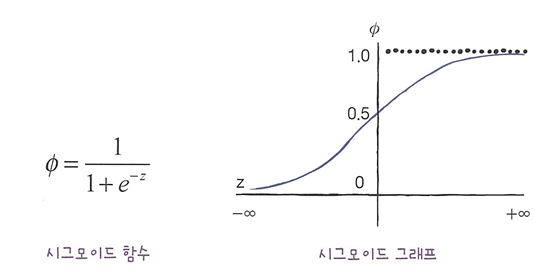
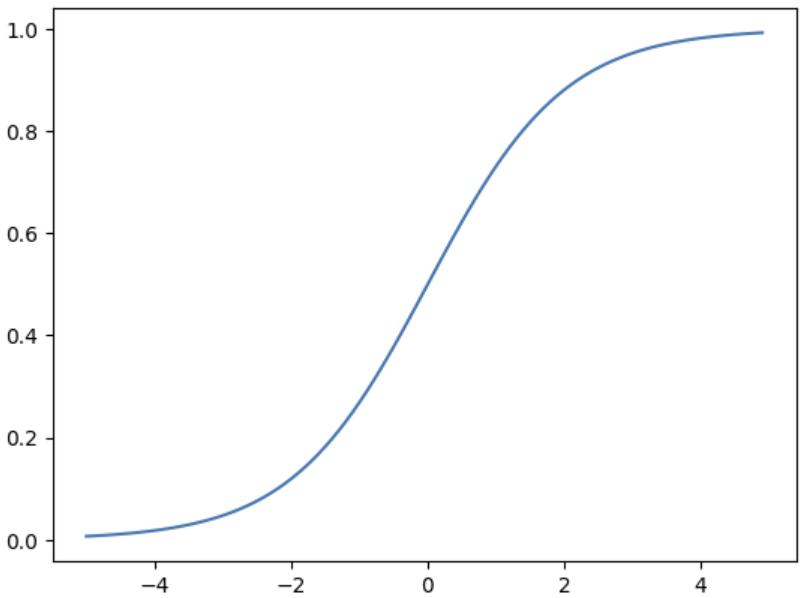
- 시그모이드 함수(로지스틱 함수)를 이용하면 z가 아주 큰 음수일 때 0, 아주 큰 양수일 때 1이 되도록 바꿀 수 있다.

넘파이로 시그모이드 함수 그래프 그리기

  
import numpy as np
import matplotlib.pyplot as plt
z = np.arange(-5, 5, 0.1)
phi = 1 / (1 + np.exp(-z))
plt.plot(z, phi)
plt.show()

로지스틱 회귀로 이진 분류 수행하기

0.5보다 큼: 양성 클래스
0.5 보다 작음: 음성 클래스
0.5: 라이브러리마다 다르다. 사이킷런은 음성 클래스로 판단.
불리언 인덱싱: 넘파이 배열은 True, False 값을 전달하여 행을 선택할 수 있다.

  
char_arr = np.array(['A', 'B', 'C', 'D', 'E'])
print(char_arr[[True, False, True, False, False]])
# ['A' 'C']

🔖 도미와 빙어의 행만 골라보자!

  
bream_smelt_indexes = (train_target == 'Bream') | (train_target == 'Smelt')
# train_target == 'Bream'에서는 train_target 배열에서 'Bream'인 것은 True이고 그 외는 모두 False인 배열을 반환한다.
# 위의 코드를 수행하면 or 연산자에 의해 도미와 빙어는 true가 되고 나머지는 false가 된다.
train_bream_smelt = train_scaled[bream_smelt_indexes]
target_bream_smelt = train_target[bream_smelt_indexes]

🔖 로지스틱 회귀 모델 훈련

  
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr.fit(train_bream_smelt, target_bream_smelt)
print(lr.predict(train_bream_smelt[:5]))
# ['Bream' 'Smelt' 'Bream' 'Bream' 'Bream']
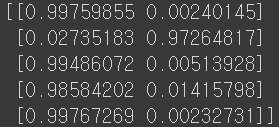
print(lr.predict_proba(train_bream_smelt[:5]))
# 왼쪽(도미): 음성 / 오른쪽(빙어): 양성

🔖 로지스틱 회귀가 학습한 계수 확인

  
print(lr.coef_, lr.intercept_)
# [[-0.4037798  -0.57620209 -0.66280298 -1.01290277 -0.73168947]] [-2.16155132]

따라서
z = -0.404 x (weight) - 0.576 x (Length) - 0.663 x (Diagonal) - 1.013 x (Height) - 0.732 x (Width) - 2.161

🔖 z 값 계산해보기

  
decisions = lr.decision_function(train_bream_smelt[:5])
# z 값 출력
print(decisions)
# [-6.02927744  3.57123907 -5.26568906 -4.24321775 -6.0607117 ]

from scipy.special import expit
# expit()는 시그모이드 함수
print(expit(decisions))
# [0.00240145 0.97264817 0.00513928 0.01415798 0.00232731]
# predict_proba() 메서드 출력의 두 번째 열의 값과 동일합니다. 따라서 decision_function()는 양성 클래스에 대한 z 값을 반환.

로지스틱 회귀로 다중 분류 수행하기

🔖 LogisticRegression 클래스로 다중 분류 모델 훈련

  
lr = LogisticRegression(C=20, max_iter=1000)
lr.fit(train_scaled, train_target)
print(lr.score(train_scaled, train_target))
print(lr.score(test_scaled, test_target))
# 0.9327731092436975
# 0.925

max_iter = 반복 횟수 지정
C: LogisticRegression에서 규제를 제어
- LogisticRegression은 기본적으로 릿지 회귀와 같이 계수의 제곱을 규제한다.(L2 규제)
- C는 alpha와 반대로 작을수록 규제가 커진다.

  
print(lr.predict(test_scaled[:5]))
# ['Perch' 'Smelt' 'Pike' 'Roach' 'Perch']
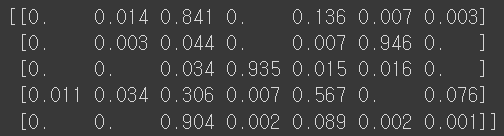
proba = lr.predict_proba(test_scaled[:5])
print(np.round(proba, decimals=3))

🔖 다중 분류일 경우 선형 방정식

  
print(lr.coef_.shape, lr.intercept_.shape)
# (7, 5) (7,)

coef와 intercept는 열이 7개 => 클래스마다 z값을 7개 계산!
이 7개의 z값을 소프트맥스 함수를 이용해 확률로 변환
- 소프트맥스: 시그모이드 함수는 하나의 선형 방정식의 출력값을 0~1 사이로 압축. 소프트맥스 함수는 여러 개의 선형 방정식의 출력값을 0~1 사이로 압축하고 전체 합이 1이 되도록 만든다.
- 지수 함수를 이용하기 때문에 정규화된 지수 함수라고 한다.

🔖 소프트맥스 함수

먼저 7개의 z값을 사용해 지수함수를 계산해 모두 더한다.

각 지수함수를 e_sum으로 나누어 준다.

  
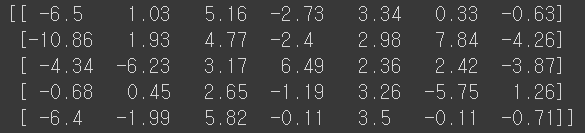
# z1~z7 까지의 값 구하기
decision = lr.decision_function(test_scaled[:5])
print(np.round(decision, decimals=2))

  
# 소프트맥스 함수 이용
from scipy.special import softmax
proba = softmax(decision, axis = 1)
# axis = 1은 계산할 축을 정하는 것이다. 1은 각 행, 즉 각 샘플에 대해 소프트맥스를 계산한다. 만약 axis 매개변수를 지정하지 않으면 배열 전체에 대해 소프트맥스를 계산한다.
print(np.round(proba, decimals=3))

정리

키워드

로지스틱 회귀: 선형 방정식을 이용한 분류 알고리즘. 시그모이드 함수나 소프트맥스 함수를 사용하여 클래스 확률을 출력할 수 있다.
다중 분류: 타깃 클래스가 2개 이상인 분류 문제. 소프트맥스 함수를 이용해 클래스 예측
시그모이드 함수: 선형 방정식의 출력을 0과 1 사이의 값으로 압축하며 이진 분류를 위해 이용한다.
소프트맥스 함수: 다중 분류에서 여러 선형 방정식의 출력 결과를 정규화하여 합이 1이 되도록 한다.

핵심 패키지와 함수

LogisticRegression
- solver: ‘lbfgs’, ‘sag(확률적 평균 경사 하강법)’
- penalty: L2 or L1 선택(기본은 ‘l2’)
- C: 규제의 강도 제어
predict_proba(): 예측 확률을 반환.
- 이진 분류: 샘플마다 음성 클래스와 양성 클래스에 대한 확률 반환.
- 다중 분류: 샘플마다 모든 클래스에 대한 확률 반환.
decision_function(): 모델이 학습한 선형 방정식의 출력을 반환.
- 이진 분류: 양성 클래스의 확률이 반환된다. 이 값이 0보다 크면 양성, 작거나 같으면 음성 클래스로 예측.
- 다중 분류: 각 클래스마다 선형 방정식을 계산.

4.2 확률적 경사 하강법

점진적인 학습

점진적 학습: 이전에 훈련한 모델을 버리지 않고 새로운 데이터에 대해서만 조금씩 더 훈련하도록 하는 학습 방법.
- 확률적 경사 하강법

확률적 경사 하강법

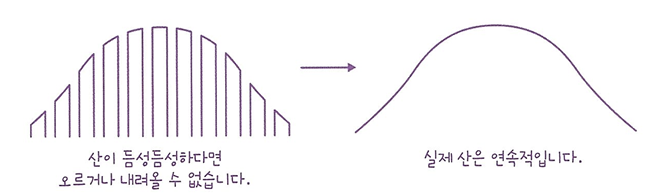
경사 하강법: 가장 가파른 경사를 따라 원하는 지점에 도달하는 것이 목표. 하지만 이때 적당히 조금씩 내려와야 한다.
확률적: 가장 가파른 길을 찾는 방법. 훈련 세트를 사용해 모델을 훈련하기 때문에 경사 하강법도 훈련 세트를 사용하여 가장 가파른 길을 찾는다. 이때 전체 샘플을 사용하지 않고 딱 하나의 샘플을 훈련 세트에서 랜덤하게 골라 가장 가파른 길을 찾는다.
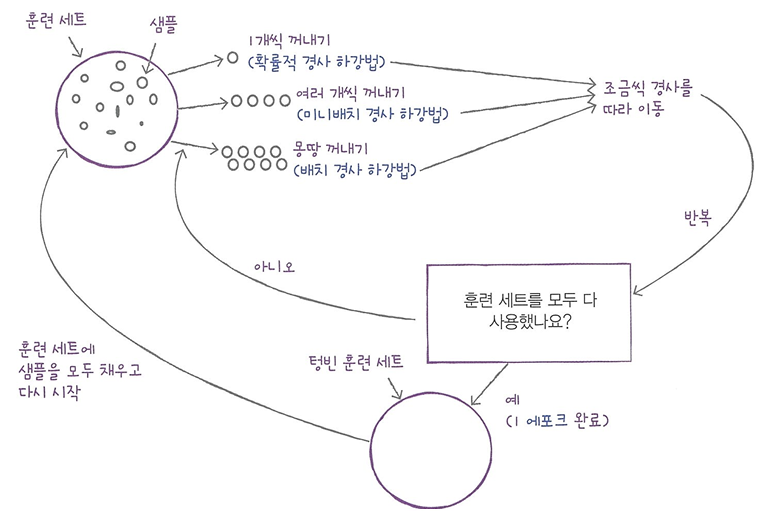
=> 훈련 세트에서 랜덤하게 하나의 샘플을 선택하여 가파른 경사를 조금 내려갑니다. 그다음 훈련 세트에서 랜덤하게 또 다른 샘플을 하나 선택하여 경사를 조금 내려갑니다. 전체 샘플을 이용할 때까지 계속합니다.
=> 만약 다 내려오지 못했다면? 다시 처음부터!
에포크: 훈련 세트를 한 번 모두 사용하는 과정.
미니배치 경사 하강법: 1개의 샘플 말고 여러 개의 샘플을 사용해 경사 하강법을 수행하는 방식.
배치 경사 하강법: 한 번 경사로를 따라 이동하기 위해 전체 샘플을 이용.(컴퓨터 자원이 많이 이용됨.)

🔖 확률적 경사 하강법과 신경망 알고리즘

신경망 알고리즘
- 확률적 경사 하강법(or 미니캐치 경사 하강법)을 꼭 이용.
- 많은 데이터를 사용하기 때문에 한 번에 모든 데이터를 이용하기 어려움.
- 모델이 복잡해 수학적 방법으로 해답을 얻기 어려움.

손실 함수

손실 함수: 머신러닝 알고리즘이 얼마나 엉터리인지 측정하는 기준(비용 함수와 엄격히 구분하지 않고 섞어서 이용)
- 손실 함수는 미분 가능해야 한다!

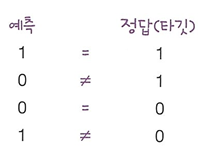
로지스틱 손실 함수(이진 크로스엔트로피 손실 함수)

예측 확률과 클래스의 타깃을 곱한 값에 음수를 취한것이 손실 함수의 값이다.
타깃이 음성 클래스 0일때는 예측 확률을 1에서 빼서 양성 클래스로 예측할 확률로 바꾸고 1(양성 클래스)을 곱한다.
예측 확률에 로그 함수를 적용하면 더 좋다. 0에 가까울 수록 아주 큰 음수가 되기에 손실을 아주 크게 만들 수 있다.
=> 로지스틱 손실 함수를 사용하면 로지스틱 회귀 모델이 만들어진다.

🔖 다중 분류의 손실함수

크로스엔트로피 손실 함수

🔖 회귀의 손실함수

평균 절댓값 오추(타깃에서 예측을 뺀 절댓값을 모든 샘플에 평균한 값)
평균 제곱 오차(타깃에서 예측을 뺀 값을 제곱한 다음 모든 샘플에 대해 평균한 값)

SGDClassifier

  
# 데이터 준비
import pandas as pd
fish = pd.read_csv('https://bit.ly/fish_csv')
fish_input = fish[['Weight', 'Length', 'Diagonal', 'Height', 'Width']].to_numpy()
fish_target = fish['Species'].to_numpy()

# 훈련 세트와 테스트 세트로 나누기
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(fish_input, fish_target, random_state = 42)

# 표준화 전처기
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)

# 확률적 경사 하강법 제공하는 대표적인 클래스
from sklearn.linear_model import SGDClassifier

# 2개의 매개변수
# loss는 손실 함수의 종류 지정 ('log' - 로지스틱 손실 함수)
# max_iter은 수행할 에포크 횟수
sc = SGDClassifier(loss = 'log_loss', max_iter = 10, random_state=42)
sc.fit(train_scaled, train_target)
# 정확도 출력
print(sc.score(train_scaled, train_target))
print(sc.score(test_scaled, test_target))
# 0.773109243697479
# 0.775

❗ 훈련 세트와 테스트 세트의 정확도가 낮다! 에포크 부족한듯
❗ ConvergenceWarning: 모델이 충분히 수렴x max_iter 늘리자!

  
# partial_fit(): 모델을 이어서 훈련할 때 이용. 호출할 때마다 1 에포크씩 이어서 훈련할 수 있음.
sc.partial_fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
print(sc.score(test_scaled, test_target))
# 0.8151260504201681
# 0.85

아직 점수가 낮지만 에포크를 한 번 더 실행하니 정확도가 향상되었습니다. 여러 에포크에서 더 훈련할 필요가 있어 보이네요. 무작정 반복할 수는 없으니 어떤 기준이 필요하겠군요.

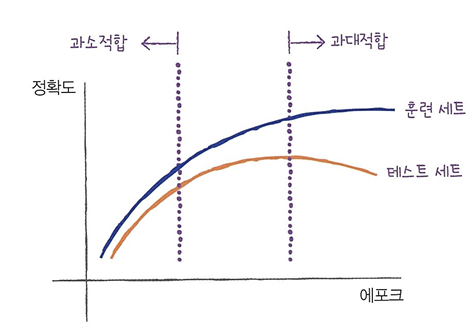
에포크와 과대/과소 적합

적은 에포크 횟수 -> 과소 적합
너무 많은 에포크 횟수 -> 과대 적합

조기 종료: 과대 적합이 시작하기 전에 훈련을 멈추는 것(테스트 세트 점수가 감소하기 시작하는 시점이 과대적합)

  
import numpy as np
sc = SGDClassifier(loss='log_loss', random_state=42)
train_score = [] # 훈련 세트 점수
test_score = [] # 테스트 세트 점수

# partial_fit() 메서드만 사용하려면 훈련 세트에 있는 전체 클래스의 레이블을 partial_fit() 메서드에 전달해 주어야 합니다.
classes = np.unique(train_target) 

# 반복마다 훈련 세트와 테스트 세트의 점수 계산
# _는 나중에 사용하지 않고 버리는 값을 넣어두는 용도
for _ in range(0, 300):
    sc.partial_fit(train_scaled, train_target, classes=classes)
    train_score.append(sc.score(train_scaled, train_target))
    test_score.append(sc.score(test_scaled, test_target))

# 점수 그래프
import matplotlib.pyplot as plt
plt.plot(train_score)
plt.plot(test_score)
plt.show()

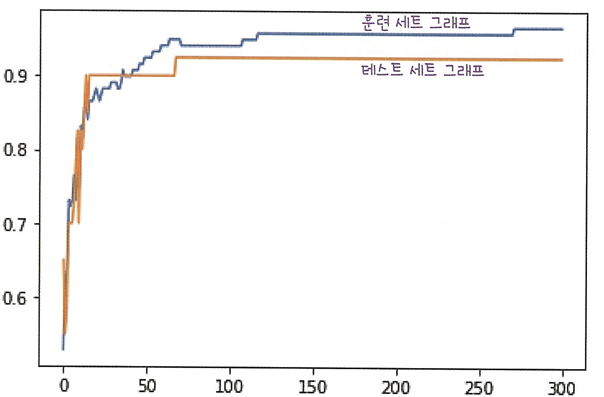❗ 100 전에는 과소적합, 100 후에는 훈련 세트와 테스트 세트의 격차가 벌어지고 있으니 100이 가장 적절.

  
sc = SGDClassifier(loss = 'log_loss', max_iter = 100, tol = None, random_state=42)
# SGDClassifier는 일정 에포크 동안 성능이 향상되지 않으면 훈련을 멈춘다. tol 매개변수에서 향상될 최솟값을 지정한다. None으로 지정하면 max_iter 만큼 무조건 반복한다.
sc.fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
print(sc.score(test_scaled, test_target))
# 0.957983193277311
# 0.925

loss 매개변수

loss 매개변수의 기본값은 ‘hinge’
- 힌지 손실은 서포트 벡터 머신이라 불리는 머신러닝 알고리즘의 손실 함수

❗ SGDClassifier가 여러 종류의 손실 함수를 loss 매개변수에 지정하여 다양한 머신러닝 알고리즘을 지원한다.

🔖 힌지 손실 이용

  
sc = SGDClassifier(loss='hinge', max_iter=100, tol=None, random_state=42)
sc.fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
print(sc.score(test_scaled, test_target))
# 0.9495798319327731
# 0.925

정리

키워드

확률적 경사 하강법: 훈련 세트에서 샘플 하나씩 꺼내 손실 함수의 경사를 따라 최적의 모델을 찾는 알고리즘.
미니배치 경사 하강법: 샘플을 여러개 이용.
배치 경사 하강법: 전체 샘플을 이용.
손실 함수: 확률적 경사 하강법이 최적화할 대상.
에포크: 확률적 경사 하강법에서 전체 샘플을 모두 사용하는 한 번 반복을 의미

핵심 패키지와 함수

SGDClassifier
- loss 매개변수: 손실 함수 지정
- penalty: 규제의 종류 지정.
- max_iter: 에포크 횟수
- tol: 반복을 멈출 조건. n_iter_no_change에서 지정한 에포크 동안 손실이 tol 만큼 줄어들지 않으면 중단.
SGDRegressor: 회귀 모델.
- loss

방학 ML 세션, 혼자 공부하는 머신러닝+딥러닝

Khuda ML data

This post is licensed under CC BY 4.0 by the author.