Ch5.dfs,bfs

Posted Aug 1, 2025 Updated Aug 1, 2024

By Lee Jae Hui

11 min read

Ch5.dfs,bfs

1. 꼭 필요한 자료구조 기초

탐색
- 많은 양의 데이터 중에서 원하는 데이터를 찾는 과정.
- 그래프, 트리 등의 자료구조 안에서 탐색을 하는 문제를 주로 다룸.
- 대표적 탐색 알고리즘: DFS, BFS
자료구조
- 데이터를 표현하고 관리하고 처리하기 위한 구조
- 스택과 큐
  - 삽입(Push)
  - 삭제(Pop)
  - 오버플로, 언더플로(아무것도 없는데 삭제 수행)

스택

First in Last out 구조 (후입선출 구조)

  
stack = []

stack.append(5)
stack.append(2)
stack.append(3)
stack.append(7)
stack.pop()
stack.append(1)
stack.append(4)
stack.pop()

print(stack) # 최하단 원소부터 출력
print(stack[::-1]) # 최상단 원소부터 출력

별도의 라이브러리 이용X List 이용!!

큐

First in First out 구조 (선입선출 구조)

  
from collection import deque

queue = deque()

queue.append(5)
queue.append(5)
queue.append(5)
queue.append(5)
queue.popleft()
queue.append(5)
queue.append(5)
queue.popleft()

print(queue)
queue.reverse()
print(queue)

별도의 라이브러리 이용o(collection 모듈에서 제공하는 deque 자료구조 활용)
list(queue)를 하면 리스트 자료형이 반환.

재귀 함수

재귀 함수: 자기 자신을 다시 호출하는 함수

  
def recursive_function():
  print('재귀 함수를 호출합니다.')
  recursive_function()

recursive_function()

무한대로 재귀 호출 진행X (파이썬 인터프리터는 호출 횟수 제한이 있음.)

재귀함수의 종료 조건

무한 호출 방지하기 위해, 재귀 함수가 언제 끝날지, 종료 조건을 꼭 명시해야 한다.

  
def recursive_function(i):
  if i == 100:
    return
  print(i, '번째 재귀함수에서', i+1, '번째 호출합니다')
  recursive_function(i+1)
  print(i, '번째 종료')

recursive_function(1)

컴퓨터 내부에서 재귀 함수의 수행 -> 스택 자료구조 이용.
- 함수 호출 시 가장 마지막에 호출한 함수가 먼저 수행을 끝내야 앞의 함수 수행.
⭐재귀 함수 = 스택 자료구조
=> 따라서 스택 자료구조를 활용해야 하는 상당수 알고리즘은 재귀 함수 이용해서 간단하게 구현 가능

  
# 반복적으로 구현한 n!
def function_iterative(n):
  result = 1
  # 1부터 n까지의 수를 차례대로 곱하기
  for i in range(1, n+1):
    result += i
  return result

# 재귀적으로 구현한 n!
def factorial_recursive(n):
  if n <= 1:
    return 1
  return n * factorial_recursive(n-1)

재귀 함수 이용의 장점
- 간결 -> 점화식(특정한 함수를 자신보다 더 작은 변수에 대한 함수와의 관계로 표현한 것)

+ 팩토리얼을 수학적 점화식으로?

1. n이 0혹은 1일때: factorial(n) = 1 -> 종료 조건
2. n이 1보다 클 때: factorial(n) = n x factorial(n - 1)

2. 탐색 알고리즘 DFS/BFS

DFS -> 스택 이용

DFS: 깊이 우선 탐색. 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘.
- 특정 경로로 탐색하다가 특정한 상황에서 최대한 깊숙이 들어가서 노드를 방문한 후, 다시 돌아가 다른 경로로 탐색하는 알고리즘.
- O(N)
- 스택을 이용하기에 재귀 함수 이용하면 간결하게 구현 가능

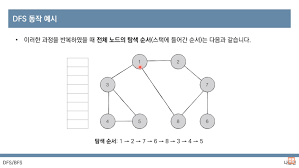
DFS의 구체적인 동작 과정
1 - 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
2 - 스택의 최상단 노드에 방문하지 않은 인접 노드가 있으면, 그 인접 노드를 스택에 넣고 방문 처리를 한다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼댄다.(인접한 노드 중 방문하지 않은게 여러가지 있다면, 번호가 낮은 순서부터 처리)
3 - 2번의 과정을 더 이상 수행할 수 없을 때까지 반복한다.

  
def dfs(graph, v, visited):
  # 현재 노드 방문 처리
  visited[v] = True
  print(v, end = ' ')
  # 현재 노드와 연결된 다른 노드를 재귀적으로 방문
  for i in graph[v]:
    if not visited[i]:
      dfs(graph, i, visited)
    
# 각 노드가 연결된 정보를 리스트 자료형으로 표현
graph = [
  [],
  [2,3,8],
  [1,7],
  [1,4,5],
  [3,5],
  [3,4],
  [7],
  [2,6,8],
  [1,7]
]

# 각 노드가 방문된 정보를 리스트 자료형으로 표현
visited = [False] * 9

dfs(graph, 1, visited)

+ 그래프의 기본 구조

- 노드(정점)와 간선으로 표현

- 그래프 탐색: 하나의 노드를 시작으로 다수의 노드를 방문하는 것

- 두 노드가 간선으로 연결되어 있다면 '두 노드는 인접하다'라고 표현

+ 그래프의 표현 방식

1. 인접 행렬: 2차원 배열로 그래프의 연결 관계를 표현
  - 연결되어 있지 않은 노드끼리는 무한의 비용이라 작성.

2. 인접 리스트: 리스트로 그래프의 연결 관계를 표현하는 방식
  - 모든 노드에 연결된 노드에 대한 정보를 차례대로 연결하여 저장.
  - '연결 리스트'라는 자료구조 이용해 구현(파이썬에선 2차원 리스트 이용)

  
# 1. 인접행렬 방식
INF = 99999999

graph = [
  [0,7,5],
  [7,0,INF],
  [5,INF,0]
]

print(graph)

  
# 2. 인접 리스트 방식 예제
# 행이 3개인 2차원 리스트로 인접 리스트 표현
graph = [[] for _ in range(3)]

# 노드 0에 연결된 노드 정보 저장(노드, 거리)
graph[0].append((1,7))
graph[0].append((2,5))

graph[1].append((0,7))

graph[2].append((0,5))

print(graph)

| | 메모리 | 속도 |특정 노드와 연결된 모든 노드 순회하는 경우| |—|—|—|—| | 인접 행렬 | 노드 개수 많을 수록 메모리 낭비| 빠름 |느림| | 인접 리스트 | 메모리 효율적 | 관계 찾는 속도 느림 |빠름|

BFS -> 큐 이용

BFS: 너비 우선 탐색. 가까운 노드부터 탐색하는 알고리즘.
- 큐 이용이 정석 -> 인접한 노드를 반복적으로 큐에 넣도록 알고리즘을 작성하면, 자연스럽게 먼저 들어온 것이 먼저 나가게 되어, 가까운 노드부터 탐색을 진행!
- O(N)
- ⭐일반적으로 실제 수행 시간은 DFS보다 좋은 편.
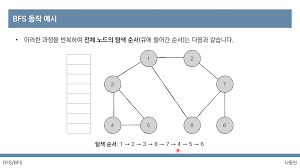
  BFS의 구체적인 동작 과정
  1 - 탐색 시작 노드를 큐에 삽입하고 방문 처리를 한다..
  2 - 큐에서 노드를 꺼내 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리를 한다.
  3 - 2번의 과정을 더 이상 수행할 수 없을 때까지 반복한다.

  
from collections import deque

def bfs(graph, start, visited):
  queue = deque([start])
  visited[start] = True
  while queue:
    v = queue.popleft()
    print(v, end=' ')
    for i in graph[v]:
      if not visited[i]:
        queue.append(i)
        visited[i] = True

# 각 노드가 연결된 정보를 리스트 자료형으로 표현
graph = [
  [],
  [2,3,8],
  [1,7],
  [1,4,5],
  [3,5],
  [3,4],
  [7],
  [2,6,8],
  [1,7]
]

# 각 노드가 방문된 정보를 리스트 자료형으로 표현
visited = [False] * 9

bfs(graph, 1, visited)

DFS와 BFS 정리

| | DFS | BFS | |–|—–|—–| |동작원리|스택|큐| |구현 방법|재귀 함수 이용|큐 자료구조 이용|

DFS와 BFS 설명하는 데 전형적인 그래프 그림 이용
1차원 배열이나 2차원 배열 또한 그래프 형태로 생각하면 수월하게 문제 풀 수 있음
=> ⭐코딩 테스트 중 2차원 배열에서의 탐색 문제를 만나면 이렇게 그래프 형태로 바꿔서 생각하면 풀이 방법을 조금 더 쉽게 떠올릴 수 있다.

책 정리, 이것이 취업을 위한 코딩 테스트다.

This post is licensed under CC BY 4.0 by the author.