Ch6.정렬

1. 기준에 따라 데이터를 정렬

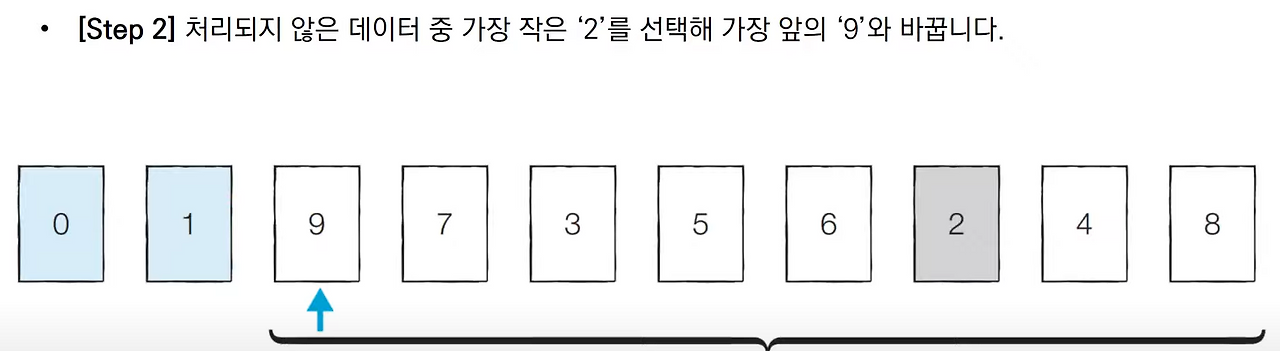
정렬 알고리즘 개요

• 정렬: 데이터를 특정한 기준에 따라서 순서대로 나열
  • 이진 탐색의 전처리 과정
  • 선택 정렬, 삽입 정렬, 퀵 정렬, 계수 정렬

    선택 정렬

• 매번 가장 작은 것을 선택.

array = [7, 5, 9, 0, 3, 1,  6, 2, 4, 8]

for i in range(len(array)):
    min_index = 1
    for j in range(i + 1, len(array)):
        if array[min_index] > array[j]:
            min_index = j
    array[i], array[min_index] = array[min_index], array[i] # 파이썬 스와프 소스코드

print(array)

선택 정렬의 시간 복잡도

• 연산 횟수: N + (N -1) + (N - 2) + — + 2 => O(N^2)
• 코딩 테스트에서 특정한 리스트에서 가장 작은 데이터를 찾는 일이 잦으므로 익숙해질 필요가 있음.

삽입 정렬

• 특정한 데이터를 적절한 위치에 삽입!
• 특정한 데이터가 적절한 위치에 들어가기 이전에, 그 앞까지의 데이터는 이미 정렬되어 있다고 가정.
• 정렬되어 있는 데이터 리스트에서 적절한 위치를 찾은 뒤에, 그 위치에 삽입됨.
• 삽입 정렬은 두 번째 데이터부터 시작!
  • 필요할 때만 위치를 바꾸므로 ‘데이터가 거의 정렬 되어 있을 때’ 훨씬 효율적

• 정렬이 이루어진 원소는 항상 오름차순을 유지.
  • 삽입될 데이터보다 작은 데이터를 만나면 그 위치에서 멈춤!

array = [7, 5, 9, 0, 3, 1,  6, 2, 4, 8]

for i in range(1, len(array)):
    for j in range(i, 0, -1):
        if array[j] < array[j - 1]:
            array[j], array[j - 1] = array[j - 1], array[j]
        else:
            break
print(array)

삽입 정렬의 시간 복잡도

• O(N^2) -> 최선의 경우 O(N)
• 현재 리스트의 데이터가 거의 정렬되어 있는 상태라면 매우 빠르게 동작

퀵 정렬(가장 많이 이용됨)

*참고: 퀵 정렬과 비교할 만큼 빠른 알고리즘으로 “병합 정렬” 알고리즘이 있다

• 정렬 라이브러리의 근간이 되는 알고리즘임.
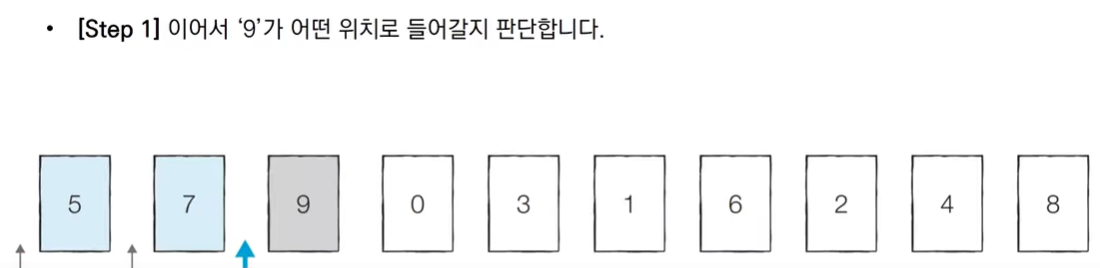
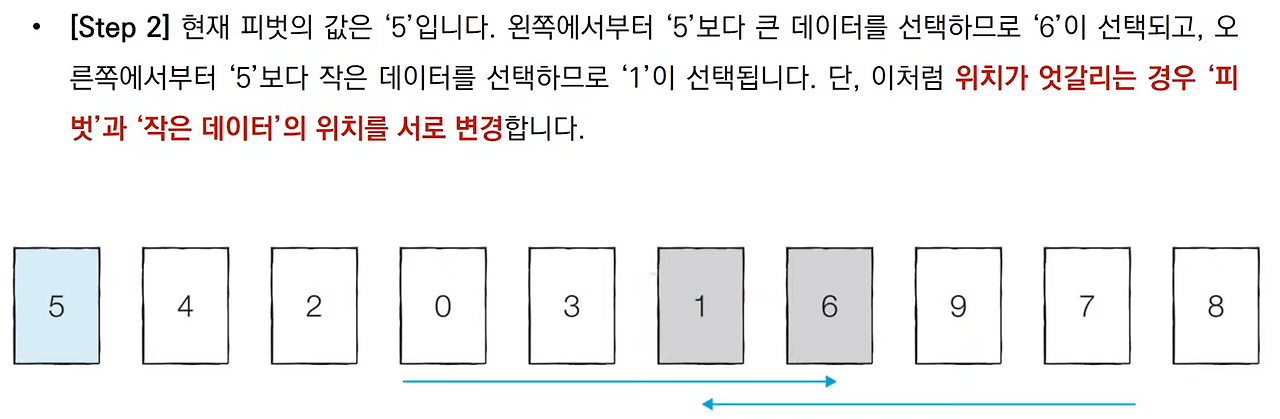
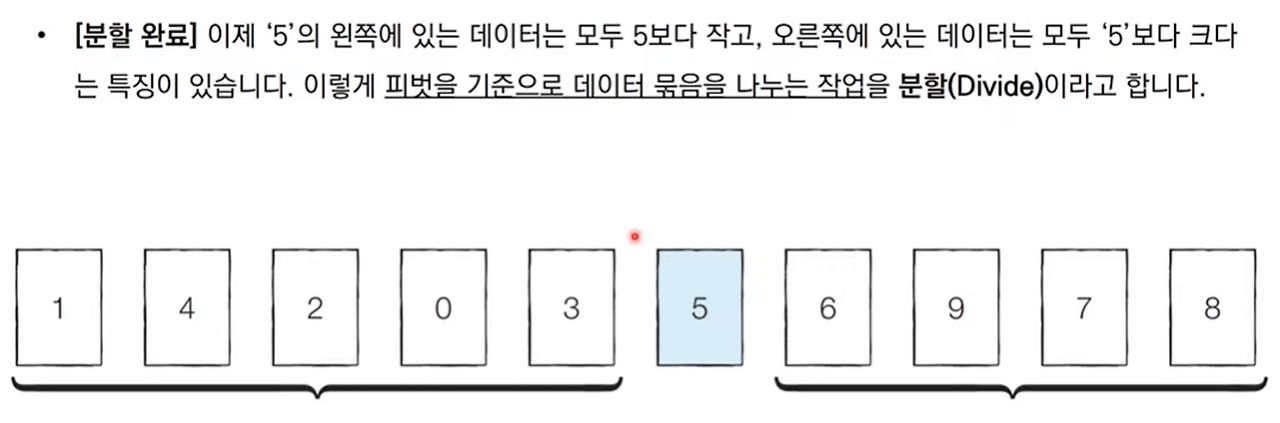
• 기준 데이터를 설정하고 그 기준보다 큰 데이터와 작은 데이터의 위치를 바꾸자
• 퀵정렬: 기준을 설정 -> 다음 큰 수와 작은 수를 교환한 후 리스트를 반으로 나누는 방식.
  • 피벗(큰 숫자와 작은 숫자를 교환할 때, 교환하기 위한 ‘기준’)이 이용됨
  • 호어 분할 방식
    1. 리스트에서 첫 번째 데이터를 피벗으로 정함
    2. 왼쪽에서부터 피벗보다 큰 데이터를 찾고, 오른쪽에서부터 피벗보다 작은 데이터를 찾는다.
    3. 큰 데이터와 작은 데이터의 위치를 서로 교환

    ⭐파티션(or 분할): 피벗의 왼쪽에는 피벗보다 작은 데이터가 위치, 오른쪽에는 피벗보다 큰 데이터가 위치
    

  • ‘재귀 함수’형태로 작성
    • 끝 조건: 현재 리스트의 데이터 개수가 1개인 경우

[Ver1]

array = [5,7,9,0,3,1,6,2,4,8]

def quick_sort(array, start, end):
    if start >= end:
        return
    pivot = start
    left = start + 1
    right = end
    while left <= right:
        while left <= end and array[left] <= array[pivot]:
            left += 1
        while right > start and array[right] >= array[pivot]:
            right += 1
        if left > right:
            array[right], array[pivot] = array[pivot], array[right]
        else:
            array[left], array[right] = array[right], array[left]
    quick_sort(array, start, right-1)
    quick_sort(array, right+1, end)

quick_sort(array, 0, len(array)-1)
print(array)

[Ver2]

array = [5,7,9,0,3,1,6,2,4,8]

def quick_sort(array):
    if len(array) <= 1:
        return array
    
    pivot = array[0]
    tail = array[1:]

    left_side = [x for x in tail if x <= pivot]
    right_side = [x for x in tail if x > pivot]

    return quick_sort(left_side) + [pivot] + quick_sort(right_side)

print(quick_sort(array))

퀵 정렬의 시간 복잡도

• O(NlogN) -> 평균적
• O(N^2) -> 최악의 경우
• 데이터가 이미 정렬되어있는 경우 매우 느리게 동작(삽입정렬이 더 빠름)

계수 정렬

• 계수 정렬: 특정한 조건이 부합할 때만 사용할 수 있지만 매우 빠른 정렬 알고리즘
• 데이터의 개수가 N, 데이터 중 최댓값이 K -> o(N+K)를 보장
• 이용 조건
  • 양의 정수일 때만 이용 가능.
  • 가장 큰 데이터와 가장 작은 데이터의 차이가 1,000,000을 넘지 않을 때
    => why? 계수 정렬을 이용할 때는 ‘모든 범위를 담을 수 있는 크기의 리스트를 선언’해야 해서
• 비교 기반의 정렬 알고르즘X 별도의 리스트를 선언하고 그 안에 정렬에 대한 정보를 담는다.
  
  
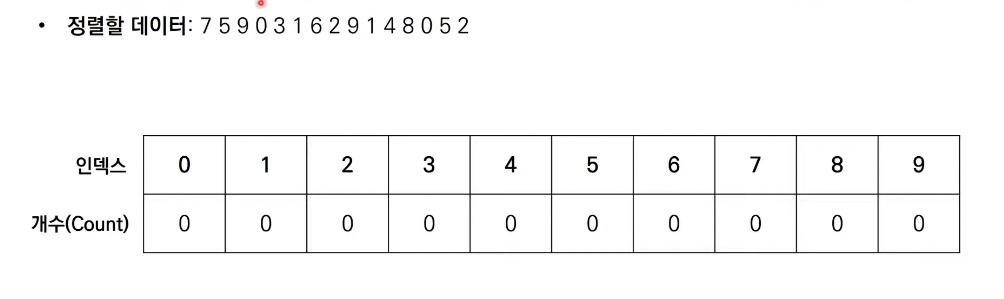
  1. 리스트 선언(ex. 가장 작은 수가 0이고, 가장 큰 수가 9이면 크기가 10인 리스트를 선언)
  2. 리스트의 모든 데이터가 0이 되도록 초기화
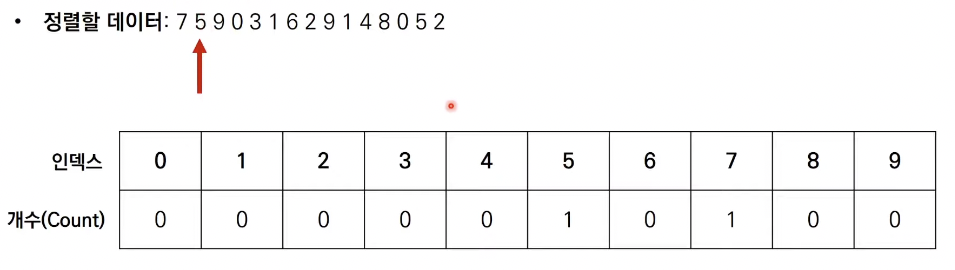
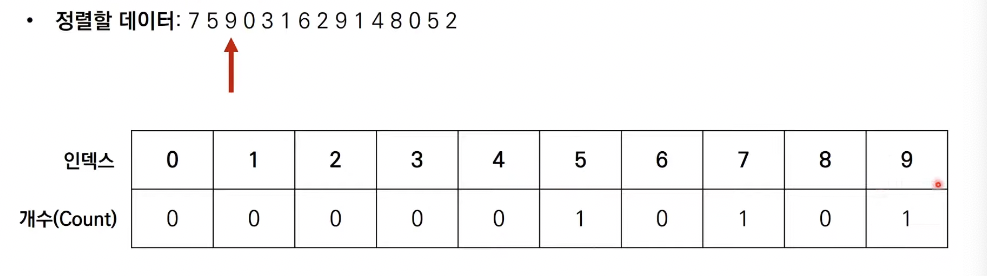
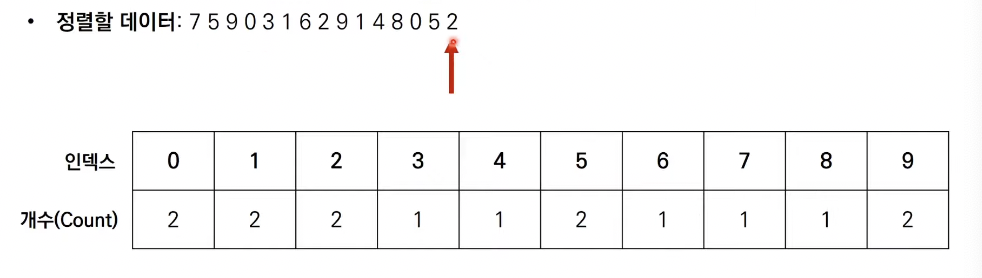
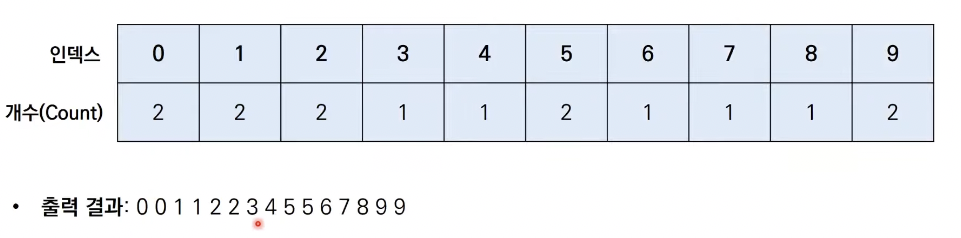
  3. 데이터를 하나씩 확인하며 데이터의 값과 동일한 인덱스의 데이터를 1씩 증가시키면 계수 정렬이 완료됨.

1. 결과를 출력할때는 리스트의 첫 번째 데이터부터 하나씩 그 값만큼 반복하여 인덱스 출력.

array = [7,5,9,0,3,1,6,2,9,1,4,8,0,5,2]

count = [0] * (max(array) + 1)

for i in range(len(array)):
    count[array[i]] += 1

for i in range(len(count)):
    for j in range(count[i]):
        print(i, end=' ')

계수 정렬의 시간 복잡도

• O(N+K)

계수 정렬의 공간 복잡도

• 계수 정렬은 크기가 한정되어 있고, 데이터의 크기가 많이 중복되어 있을수록 유리하다.
• O(N+K)

파이썬의 정렬 라이브러리

• sorted(): 퀵 정렬과 동작 방식이 비슷한 병합 정렬을 기반으로 만들어짐.
  • 최악의 경우에도 O(NlogN) 보장\
  • 정렬된 리스트가 반환된다.

      result = sorted(array)
    

• sort:
  • 반환X 내부 원소가 바로 정렬

      array.sort()
    

• 정렬 라이브러리에서 Key
  • key 값으로 하나의 함수가 들어감
  • 정렬 기준이 됨

array = [('바나나',2), ('사과',5), ('당근',3)]

def setting(data):
    return data[1]

result = sorted(array, key=setting)
print(result)

정렬 라이브러리의 시간 복잡도

• 최악의 경우에도 O(NlogN) 보장
• Tip
  • 문제에서 별도의 요구 X -> 라이브러리 이용
  • 범위가 한정되어 있음 -> 계수 정렬 이용

1. 정렬 라이브러리로 풀 수 있는 문제
2. 정렬 알고리즘의 원리에 대해서 물어보는 문제
3. 더 빠른 정렬이 필요한 문제